Version originale en anglais au format PDF ou HTML Traduit en mai 2002 par Joël Eymard pour http://la.trompette.free.fr
Optimisation informatique des cuivres par Wilfried Kausel (suite)
Pour le premier test, une trompette typique a été modifiée localement de façon à perturber ses propriétés acoustiques normales. On a inséré un goulot d'étranglement artificiel près de l'embouchure, au début de la branche d'embouchure, là où les cuivres sont très sensibles aux modifications de géométrie. On a donné comme objectif d'impédance la courbe d'impédance originale de l'instrument à l'optimiseur. Les diamètres de perce au voisinage de la modification ont été les variables d'optimisation choisies pour permettre au programme de corriger le défaut artificiel.

Figure 2 : Trompette avec goulot d'étranglement
; impédance initiale (en rouge) et impédance objectif (en vert)
La figure 2 montre le profil de l'instrument déroulé
incluant le goulot d'étranglement avec des échelles différentes
sur les axes x et y ajustées pour permettre l'affichage
complet dans la fenêtre. Les marqueurs placés le long du profil
indiquent les points de contrôle du contour. Les graduations des axes
sont associées à l'amplitude de l'impédance d'entrée, les
unités sont le Herz et le kilohm.
Ce problème d'optimisation simple a été résolu par
tous les algorithmes dans un temps très court. A titre d'exemple la figure
3 montre le résultat d'un algorithme génétique avec développement
de population progressif. Huit paramètres de coordonnée (la spécification
de géométrie complète de la branche d'embouchure) ont été
choisis comme variables d'optimisation. Leur plage de variation a été
limitée à ± 10 millimètres en abscisse et à
± 80 % des valeurs initiales du diamètre en ordonnée.
Les paramètres de l'algorithme génétique progressif étaient
une taille de population de 100, une probabilité de croisement de 0,6,
une probabilité de mutation de 0,1 et le nombre de descendants était
de 2. Il a fallu environ 350 calculs de la fonction objectif - en termes d'optimisation
génétique : évaluation d'un individu - pour produire le
résultat illustré qui améliore la fonction objectif d'environ
36 à environ 11.
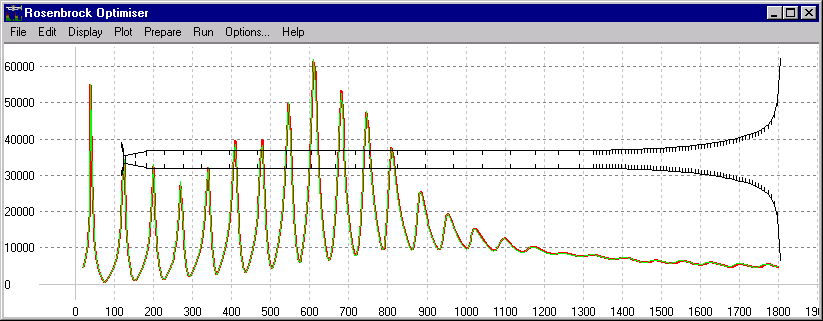
Figure 3 :
trompette corrigée créée par algorithme génétique
(version progressive)
L'algorithme génétique simple avec les mêmes
paramètres n'a pas pu améliorer une valeur initiale plutôt
bonne trouvée par hasard en plus de 12 générations et en
évaluant plus de 1200 individus.
L'algorithme stationnaire, avec toujours les mêmes paramètres et
un chevauchement de population de 50 %, a eu besoin d'environ 450 évaluations
pour approcher la solution obtenue par l'algorithme progressif.
L'algorithme Deme avec trois populations parallèles et 5 individus pour
migrer de chaque génération s'est arrêté après
avoir atteint une amélioration acceptable en 450 évaluations.
Une nouvelle amélioration a été obtenue beaucoup plus tard
après 1300 évaluations.
L'algorithme progressif avec la "cohue déterministe" a bénéficié
d'un coup de chance initial. Pendant la phase d'initialisation aléatoire,
il a trouvé une bonne solution en 30 tentatives seulement. Il a eu besoin
de 500 évaluations supplémentaires pour trouver une nouvelle amélioration.
L'algorithme de Rosenbrock n'a pas eu besoin de plus de 130 calculs de la fonction
objectif pour battre le résultat de n'importe quel algorithme génétique
et il a pris 120 autres évaluations pour produire un résultat
d'optimisation 10 fois meilleur que le meilleur génétique.
De toute façon ces résultats étaient valables et assez
encourageants pour lancer un travail vraiment sérieux. Les différents
algorithmes devaient maintenant montrer leur capacité à fonctionner
avec un grand nombre de variables ; en fait la géométrie complète
de l'instrument devait maintenant être soumise à l'optimisation.
D'autre part le problème devait être soluble et le résultat
optimum être connu. En même temps il fallait prouver même
au sceptique qu'il y a un rapport clair entre la courbe d'impédance d'entrée
et la géométrie de cet instrument.
Donc le test ultime pour tous les algorithmes était de construire une
trompette avec une impédance d'entrée donnée en partant d'un tube
étroit muni d'une embouchure standard. On voit cette situation initiale
à la Figure 4. Tous les diamètres de perce sur la longueur totale
de l'instrument ont été pris comme variable d'optimisation, avec
une limite supérieure de variation de deux fois les dimensions d'une
trompette moyenne.
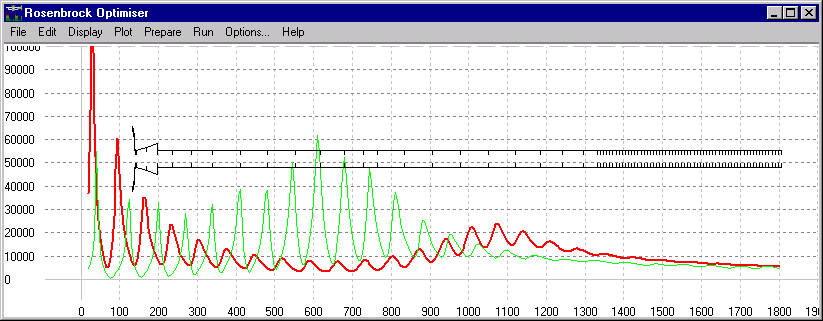
Figure 4 :
Conception d'une trompette à partir de zéro
Quand une courbe d'impédance mesurée est utilisée comme objectif,
on a ce qu'on appelle dans la littérature "le problème inverse"
ou "la reconstruction de la perce". Jusqu'ici ce problème inverse
n'a été abordé et résolu avec succès que
sur la base d'une réponse impulsionnelle mesurée dans le domaine
du temps.
Bien que l'on sache qu'une réponse impulsionnelle dans le domaine du
temps est mathématiquement l'équivalent exact d'un spectre complexe
dans le domaine des fréquences, on n'avait pas encore envisagé
d'utiliser la mesure d'un état stable dans le domaine des fréquences
comme base d'une reconstruction du profil de perce. La raison est que le système
qui est examiné dans ce qu'on appelle la "réflexométrie
d'impulsion"
[14]
[15]
et celui qui est mesuré d'habitude par les
méthodes du domaine des fréquence ne sont pas complètement
identiques.
Dans la "réflexométrie d'impulsion" l'instrument est
couplé à une source sonore non réfléchissante. Cela
signifie idéalement que le front d'onde plane de l'impulsion de Dirac
est guidé dans l'instrument en passant par un tube infiniment long avec
une impédance caractéristique qui correspond parfaitement à l'impédance
caractéristique de la section circulaire au point d'entrée de
l'instrument mesuré. Toutes les réflexions qui sont observées
à ce point d'entrée sont donc causées par des variations
d'impédance (= des changements de diamètre) dans l'instrument et les
réflexions multiples causées par la terminaison au point d'entrée
sont évitées.
On le réalise pratiquement en utilisant un tube assez long depuis la
source du son pour que les réflexions de l'extrémité où
l'impulsion est déclenchée n'atteignent pas le point d'entrée
de l'instruments pendant l'intervalle de temps exigé par la mesure. Ce
qui est enregistré est la caractéristique transitoire après
une impulsion d'excitation d'un système qui était à l'équilibre
parfait auparavant.
Dans les mesures du domaine des fréquences l'état
stable est mesuré et une source de son réfléchissante est
d'habitude directement connectée à l'embouchure. Pour calculer
la réponse impulsionnelle d'entrée IIR(ejq),
q étant la fréquence discretisée,
exigée pour faire la reconstruction de la perce analytiquement, les phases
de l'impédance d'entrée Zin(ejq)
doivent être connues ou correctement reconstruites et l'impédance caractéristique
Z0 de la section efficace couplée
doit être déterminée exactement. Par-dessus le marché,
la conversion
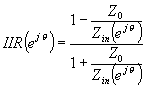
semble présenter un défi numérique pour
obtenir un résultat assez précis en vue de l'algorithme incrémental
permettant d'obtenir les dimensions physiques qui est déjà assez
sensible.
L'autre solution - utiliser l'optimiseur pour faire correspondre une courbe
d'impédance simulée et une courbe mesurée, et reconstrure ainsi
la géométrie originale - résout implicitement tous ces
problèmes. Elle peut même faire correspondre les phases, s'il s'avère
finalement que les phases apportent une information vraiment utile pour la géométrie
et elle peut travailler avec des modèles beaucoup plus généraux
et précis - incluant même les modes d'oscillation supérieurs
et d'autres sortes de pertes. Finalement il semble évident qu'il est
bien plus facile de faire des mesures sur un état stable dans le domaine
des fréquences avec une bonne précision que des mesures dans le
domaine du temps impliquant des impulsions de Dirac idéales et des tubes
d'accouplement très longs "sans perte".
Le résultat correspondant, réalisé selon la stratégie
de Rosenbrock en permettant un nombre illimité d'évaluations de
la fonction objectif (il a pris un long week-end sur un Pentium 3 à 500 MHz)
est présenté à la figure 5. Détail intéressant,
même avec un ajustement presque parfait de l'impédance obtenue
sur l'impédance cible, il reste des ondulations visibles près
de l'extrémité du pavillon. C'est certainement plus qu'une simple
coïncidence si la méthode directe de Sharp et Amir de reconstruction
de la perce à partir de réponses impulsionnelles mesurées
cesse aussi quelque part dans le pavillon de produire des coordonnées
précises.
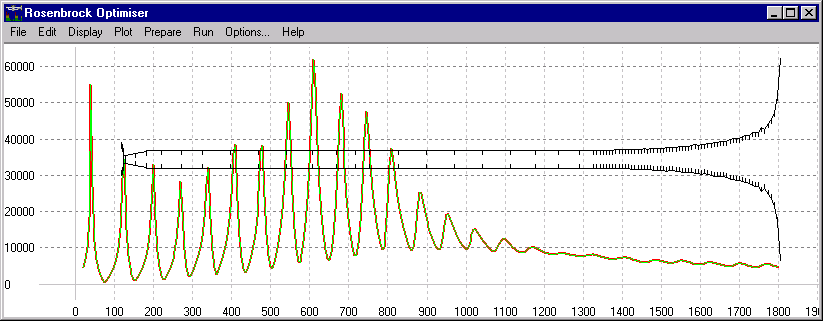
Figure 5: La trompette créée par
l'algorithme de Rosenbrock
D'abord, c'est la région où tout les modèles unidimensionnels cessent d'être valides. Deuxièmement, les mesures - et même les simulations - de réflexions faibles venant de l'extrémité éloignée, atténuée par les pertes modelisées ou non modelisées sont certainement affectées d'un peu de bruit, réel ou numérique. Le modèle de ligne de transmission multiplie le vecteur d'impédance terminal par environ cent matrices de transmission partielle pour obtenir l'impédance d'entrée. Il semble que la contribution des matrices les plus proches de l'embouchure soit plus précise ou simplement plus significative.
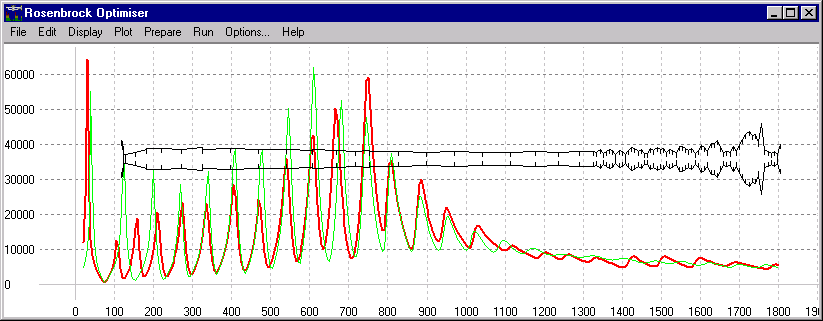
Figure 6 : La trompette créée
par l'algorithme génétique stationnaire
Malheureusement les résultats des algorithmes génétiques
ont été tous vraiment inférieurs. On voit le meilleur sur
la figure 6. Pour faire des algorithmes génétiques capables de
rivaliser, il faufrait redéfinir complètement la représentation
géométrique de l'instrument et sa configuration "génétique".
Le dernier exemple montre comment l'optimiseur traite la co-optimisation des
différentes combinaisons de valve d'une trompette réelle. La géométrie
principale a été mesurée par David Sharp (David, merci
pour cette contribution de valeur!) de l'Université d'Edimbourg en utilisant
la méthode publiée dans [14]
. Le pavillon a été mesuré avec un pied à coulisse.
La figure 7 montre comment la longueur acoustique réelle est modifiée par les valves. L'action d'une valve baisse toutes les notes jouables de un, deux ou trois demi-tons, par insertion d'un tube supplémentaire dans le trajet du son, qui l'allonge dans la proportion adéquate - environ 6 % par demi-ton. Une combinaison de valves, ajoutant par exemple 6 % et 12.36 % (1,06² = 1,1236) de la longueur originale ajoutera au total 18.36 %. C'est moins que 19.1 % (1,063 = 1,191) qui serait exigé pour baisser la note correctement de trois demi-tons. Donc une valve séparée est utilisée pour baisser de cette valeur.
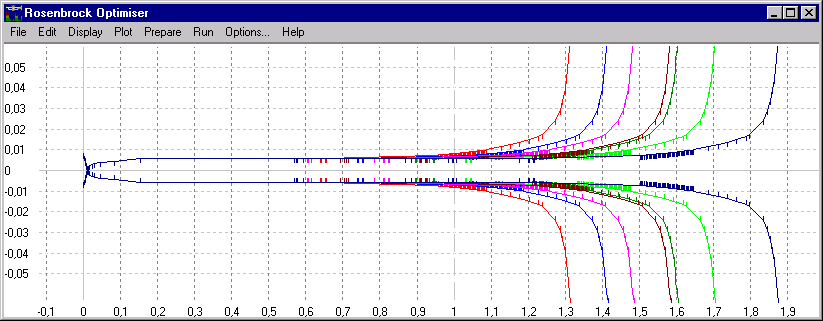
Figure 7 : Géométrie d'une trompette
en Sib correspondant à toutes les combinaisons de valves possibles
Cela ne signifie pas que les combinaisons de valves ne sont
pas utilisées par les trompettistes. Quelques notes peuvent être
obtenues seulement en combinant deux ou même trois valves, bien que la
hauteur doive être corrigée par une coulisse mobile ou avec les
lèvres. L'optimiseur a alors été utilisé pour optimiser
la justesse de toutes les notes jouables pour obtenir une justesse globale qui
soit le meilleur compromis possible incluant toutes les combinaisons de valves
La figure 8 montre les écarts de justesse de toutes les notes jouables,
mesurés en cents, avant une optimisation complète de la justesse.
La base du calcul de la justesse est la gamme à tempérament égal,
qui divise une octave en douze demi-tons égaux. Le rapport de fréquence
correspondant à l'octave est 1:2, le rapport correspondant à un
demi-ton tempéré est donc ![]() (soit une différence d'environ 6 %). Chaque demi-ton est divisée
en 100 cents, 1 cent représente un rapport de fréquence
(soit une différence d'environ 6 %). Chaque demi-ton est divisée
en 100 cents, 1 cent représente un rapport de fréquence ![]() (environ 578
millionièmes). Un écart de justesse d'environ 10 cents est d'habitude
tolérable.
(environ 578
millionièmes). Un écart de justesse d'environ 10 cents est d'habitude
tolérable.
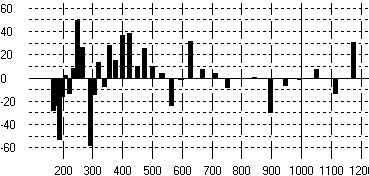
Figure 8 : écarts de justesse de toutes les
notes jouables avant optimisation
La figure 9 montre la justesse obtenue après optimisation, qui est bien meilleure et plus équilibrée que ce qu'on trouve d'habitude avec une trompette courante. En particulier les notes les plus basses de chaque combinaison de valves sont fausses sur presque tous les instruments modernes.
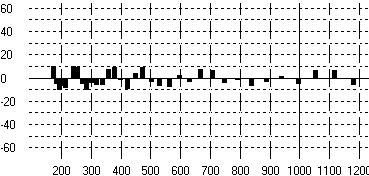
Figure 9: écarts de justesse de toutes
les notes jouables après optimisation par Rosenbrock
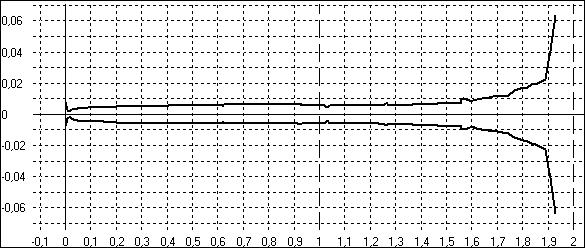
Figure 10 : géométrie obtenue après
optimisation complète de la justesse
Pour cette optimisation globale de la justesse, toutes les
coordonnées des sections ont été prises comme variables
d'optimisation. Aucune contrainte spécifique n'a été mise
sur la forme de la courbe d'impédance d'entrée, seule l'optimisation
de la justesse a été recherchée.
Il est intéressant de noter que la géométrie résultante
(figure 10) ressemble à certains instruments historiques. Y a-t-il un
savoir ancien, dont les fabricants d'instrument d'autrefois auraient été
dépositaires, qui aurait été perdu pour quelque raison
pour être maintenant retrouvé avec l'aide des ordinateurs modernes
?
Introduction
Modélisation des cuivres
Modèle de ligne de transmission
pour l'optimisation
Les différents algorithmes d'optimisation
L'algorithme de Rosenbrock
Représentation de la géométrie
de l'instrument
Calcul de l'impédance d'entrée
Objectif de la fonction d'optimisation
Résultats d'optimisations
Références