Version originale en anglais au format PDF ou HTML Traduit en mai 2002 par Joël Eymard pour http://la.trompette.free.fr
Optimisation informatique des cuivres par Wilfried Kausel (suite)
Depuis près de 80 ans, les acousticiens essayent de
prévoir le comportement de systèmes acoustiques en utilisant des
techniques de modélisation diverses
[1]
. Jusqu'à présent,
ils ont trouvé par plusieurs voies différentes comment calculer
les caractéristiques d'instruments de géométrie donnée
en utilisant des ordinateurs.
La technique de modélisation la plus complexe, la méthode des
élément fini (FEM), peut représenter l'espace à
3 dimensions et la validité de ses résultats n'est pas limitée
à une certaine gamme de fréquence
[2]
. Malheureusement cette méthode
exige considérablement plus de ressources informatiques que les autres
et n'est donc pas utilisable quand on a besoin de répéter des
calculs dans une boucle itérative.
D'un autre côté, la modélisation d'un équivalent
électrique simple [3]
ne donne pas de résultats assez précis
pour être exploitables en pratique. La modélisation par ligne de
transmission [4]
est un compromis entre le modèle simple et le modèle
FEM le plus précis. Les éléments de ligne de transmission
peuvent être tirés de segments cylindriques aussi bien que de segments
coniques et les pertes peuvent être négligées ou prises
en compte.
Des études ont montré que la modélisation par ligne de
transmission, utilisant des éléments coniques et prenant en considération
les pertes, est suffisamment précise dans la gamme de fréquence
que l'on considère normalement pour être intéressante quand
on analyse les cuivres [5]
.
D'autres auteurs utilisant des éléments de ligne de transmission
coniques pour modéliser l'impédance d'entrée de cuivres ont obtenu
un accord excellent entre les prédictions du modèle et les données
expérimentales [4]
. Les ressources en calcul exigées par cette
méthode de simulation permettent de nos jours le traitement itératif
qui est essentiel dès que la modélisation physique est employée
dans le contexte d'une optimisation informatique de cuivres du monde réel.
Modèle de ligne de transmission pour l'optimisation
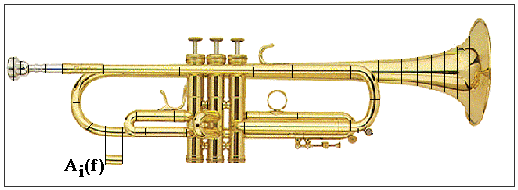
Figure 1 : Découpage de la trompette en
tranches coniques décrites par des matrices de transmission
Ce modèle de ligne de transmission utilise des tranches coniques ou cylindriques simples pour représenter l'instrument à analyser comme indiqué à la figure 1. Chaque tranche de la ligne de transmission acoustique est décrite par une matrice de transmission dépendant de la fréquence [5] qui prend en compte les pertes thermo-visco-élastiques :
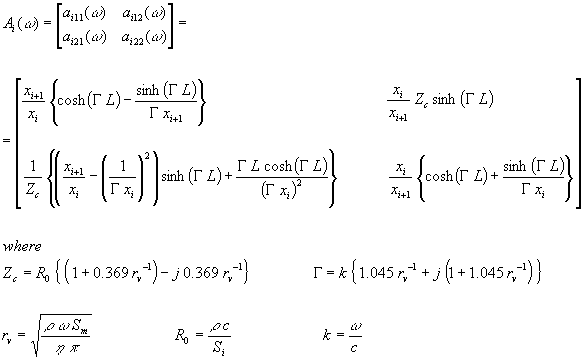
où r désigne
la densité de l'air à l'équilibre, w
la pulsation, h
le coefficient de viscosité, c la vitesse du son, Sm
la section de l'élément conique au centre, Si
la surface de la section sphérique d'entrée de l'élément
conique, xi le rayon de la section
d'entrée, xi+1 le rayon
de la section sphérique de sortie et L la distance entre
les deux sphères
La matrice suivante décrit le rapport entre la pression acoustique p
et le débit u avant et après une tranche conique
par :
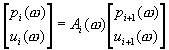
Le produit
![]()
donne une expression de la caractéristique de transmission de l'instrument complet. Le rapport entre pression acoustique et débit à l'extrémité évasée du pavillon :
![]()
est égal à l'impédance terminale (ou de radiation) ZT qui est l'impédance caractéristique de la bouche ouverte de l'instrument. Il est ici modelisé par
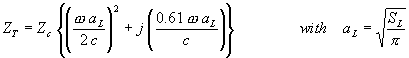
On obtient l'impédance acoustique d'entrée en
transformant cette impédance par la chaîne de matrices A
depuis l'ouverture du pavillon jusqu'à l'embouchure.
Du fait de l'hypothèse unidimensionnelle, les modes d'oscillation de
plus haute fréquence ne sont pas pris en compte par ce modèle.
Les fréquences au-dessus d'une certaine limite, qui dépend du
diamètre du tuyau, ne peuvent être couvertes par ce modèle
sans prendre en considération les modes d'oscillation transversaux. Dans
un cuivre, le pavillon est typiquement la région qui détermine
la limite de fréquence supérieure à cause de ses grandes
dimensions. La fréquence
![]()
est considérée d'habitude comme la limite supérieure de fréquence théorique pour un conduit circulaire de diamètre d, pour pouvoir ignorer les modes d'oscillation supérieurs. Dans un cuivre la limite est quelque peu réduite à cause de sa géométrie plus complexe, sa section parfois légèrement non circulaire et les courbures de son tube.
Introduction
Modélisation des cuivres
Modèle de ligne de transmission pour
l'optimisation
Les différents algorithmes d'optimisation
L'algorithme de Rosenbrock
Représentation de la géométrie
de l'instrument
Calcul de l'impédance d'entrée
Objectif de la fonction d'optimisation
Résultats d'optimisations
Références