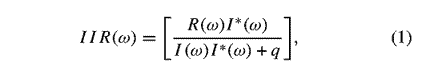Original version in English (PDF document 151 ko)
Distinguer des objets tubulaires semblables
en utilisant la réflectométrie
d'impulsion : une étude des branches d'embouchure de trompette et
de cornet.
J M Buick1, J Kemp1,
D B Sharp2, M van Walstijn1 ,
D M Campbell1 et R A Smith3
1 Département de physique et d'astronomie, JCMB, université d'Edimbourg,
route de Mayfield, Edimbourg EH9 3JZ, R-U
2 Département d’ingénierie de l’environnement et de
construction mécanique, université ouverte, Walton Hall, Milton
Keynes MK7 6AA, R-U
3 Instruments de Musique Richard Smith, 110 The Vale, Southgate, Londres N14
6AY, R-U
Reçu le 13 août 2001, mis en forme finale et admis pour la publication
le 11 mars 2002
Publié le 18 Avril 2002
En ligne à stacks.iop.org/MST/13/750
Résumé.
Cet article traite de la mesure du rayon interne d'un certain nombre
de branches d'embouchure semblables, courtes et tubulaires en utilisant la
réflectométrie
d'impulsion. La réflectométrie d'impulsion est une technique
acoustique pour mesurer la perce interne d'un objet tubulaire en analysant
les réflexions
qui se produisent quand une impulsion acoustique est envoyée dans l'objet.
Les branches d'embouchure sont conçues pour former la partie initiale
d'une trompette ou d’un cornet et leurs rayons internes diffèrent
de moins de 0,1 millimètre entre des branches semblables. On étudie
la capacité du réflectomètre à détecter
ces petites différences, qui sont considérées par les
instrumentistes comme produisant une différence apparente dans le son
d'un instrument. On voit que le réflectomètre d'impulsion peut
distinguer des branches d'embouchure avec des rayons nominaux différant
d’aussi peu que
0,03 millimètre, démontrant son potentiel dans l'étude
des instruments de musique et prouvant qu'il peut être utilisé comme
outil diagnostique par le fabricant d'instrument pour détecter des défauts
qui sont assez significatifs pour changer l’acoustique de jeu de l'instrument.
La précision
absolue des mesures de rayon est également considérée à l’extrémité de
la branche d'embouchure, où l'incertitude est de ±0,05 millimètre.
Mots-clés : réflectométrie d'impulsion acoustique, profil
de perce, branches d'embouchure.
1. Introduction.
Dans la production et l'évaluation des instruments de musique à vent,
il est très utile que le fabricant puisse étudier la perce interne,
puisque le jeu de l'instrument est déterminé en fin de compte
en grande partie par ce profil. Bien que le rapport entre la forme de perce
et l'acoustique de l'instrument soit très compliqué, la capacité à obtenir
une description détaillée du profil interne de l'instrument peut être
utile au fabricant, en particulier comme outil diagnostique permettant de faire
des comparaisons entre les « bons » et les « mauvais » instruments.
Les comparaisons de ce type peuvent indiquer exactement les endroits où le
fabricant peut intervenir pour améliorer le jeu d'un « mauvais » instrument.
Dans ce papier, nous considérons l'étude d'un certain nombre
de branches d'embouchure pour trompettes et cornets. Elles constituent la partie
initiale de la trompette ou du cornet et ont été conçues
par le fabricant avec une série de perces légèrement différentes
afin de varier les qualités musicales de l'instrument.
Pendant de nombreuses années, la perce interne des instruments de musique
a été mesurée à l'aide d’outils tels que
le pied à coulisse. Bien que ceux-ci puissent donner une mesure précise
de la perce, il n'est généralement pas possible d'accéder à la
totalité de l'instrument et on obtient ainsi un profil incomplet. Produire
un profil détaillé dans les régions accessibles exige
un grand nombre de mesures simples et peut prendre du temps. Le domaine accessible
peut être étendu en insérant des objets d'une taille connue
(ou d'une taille qui peut être mesurée avec le pied à coulisse)
dans l'instrument. Ceci peut également prendre du temps, et la région
de mesure est limitée à partie rectiligne à chaque extrémité de
l'instrument, ou au voisinage des parties qui peuvent être démontées
(par exemple la coulisse d’un trombone). En outre, les courbures dans
un tube produisent habituellement des irrégularités de perce,
et ainsi le seul moyen de mesure restant consiste à couper le tube en
tranches et à faire de nombreuses mesures de chaque tranche.
Une méthode
alternative pour obtenir des profils de perce consiste à mesurer d'abord
l'impédance d'entrée de l'instrument. Celle-ci est définie
comme le rapport de la pression acoustique au débit alternatif à l'entrée à l'instrument.
Le profil de perce et l'impédance d'entrée sont étroitement
liés et, en principe, le profil de perce peut être dérivé d'une
mesure d'impédance d'entrée. Jusqu'ici, les tentatives pour mesurer
la perce de cette manière se sont révélées difficiles.
Récemment [1] on a montré que la reconstitution de la perce à partir
de l'impédance d'entrée est faisable en utilisant une technique
d'optimisation. Cette approche est actuellement poursuivie par l'auteur de
[1]. Actuellement sa résolution le long de l'axe de l'instrument mesuré est
limitée par la bande passante du système ; la méthode
est prometteuse en terme de précision, mais cette technique exige des
ressources informatiques importantes. Dans cet article nous considérons
une troisième
technique : la réflectométrie d'impulsion acoustique.
La réflectométrie d'impulsion est une technique de mesure non-intrusive
qui peut être appliquée pour obtenir des mesures internes des
objets tubulaires. La technique a été développée
pour la première fois pour les études sismiques [2] et a été également
appliquée à la mesure des voies aériennes dans des applications
médicales [3-5]. Smith [6] a été le premier à utiliser
la réflectométrie d'impulsion pour détecter des débris
et des imperfections dans des trompettes non détectables ni mesurables
par les méthodes traditionnelles. Une imperfection de grand intérêt
pour les joueurs de cuivres est le défaut d'alignement des pistons,
et dans les essais on détectait aisément un écart de 0,25
millimètre.
Plus récemment la technique a été appliquée à l'étude
d'autres instruments de musique [7-10] aussi bien qu'à des objets tubulaires
quelconques
[7, 11, 12]. La réflectométrie d'impulsion consiste à envoyer
une impulsion sonore courte, contenant une large gamme de fréquences,
dans l'objet à mesurer. Les réflexions internes de cette impulsion
sont alors enregistrées et on obtient la réponse d'impulsion
d'entrée.
La réponse d'impulsion d'entrée peut alors être utilisée
pour calculer la perce interne [7, 11, 13, 14] de l'objet.
Les qualités musicales d'un instrument (justesse, timbre et réponse)
dépendent fortement du profil de perce de la colonne interne d'air.
Les petits cuivres, tels que la trompette ou le cornet, peuvent être
caractérisés
par trois sections principales de tube en laiton. La section la plus évidente
d'une trompette est le pavillon, qui est fixé à la partie cylindrique
(d’un diamètre d’environ 11,8 millimètres) contenant
les pistons (permettant au musicien de jouer une gamme chromatique) et la coulisse
d'accord fin à une fréquence standard. Cette section est reliée à l'extrémité de
l'embouchure (diamètre d'approximativement 7 millimètres) par
un tube conique de 250 millimètres appelé la branche d'embouchure.
Smith et Daniell [15] ont étudié l'effet sur les qualités
musicales de petits changements de l'ordre de 0,1 millimètre aux formes
de perce des trompettes. En raison d'un effet proportionnel, ces changements
ont un effet bien plus grand sur les sections de petit diamètre telles
que la branche d'embouchure que sur n'importe quelle autre partie de l'instrument,
et il ressort des essais que certains instrumentistes peuvent détecter
ces petites différences. En conséquence le fabricant de cuivres
Smith-Watkins [16] fournit à ses clients un choix de 15 profils différents
interchangeables de branche d'embouchure sur leur modèle de trompette.
Ces tubes coniques sont produits par tréfilage c.-à-d. en forçant à travers
un bloc de plomb un tube en laiton recuit enfilé sur un mandrin en acier
durci de forme spéciale. Avec le contrôle total de la fabrication
et la mesure finale de chaque branche, Smith-Watkins est certain de reproduire
le même objet réalisé initialement il y a 16 ans. En fait,
Smith a obtenu en 1999 le prix du « produit du millénaire » pour
le système interchangeable de branche d'embouchure utilisé sur
son cornet « Soloist »[16]. Un cornet a une plus longue branche
d'embouchure (approximativement 360 millimètres) qu'une trompette ;
puisque la branche d'embouchure de cornet est recourbée en un grand
demi-cercle, la mesure interne est impossible par des moyens traditionnels
tels que le pied à coulisse.
Un certain nombre de branches d'embouchure de cuivres Smith-Watkins ont été utilisées
dans cette étude. Les branches d'embouchure de trompette sont identifiées
par un numéro et sont de trois familles : {10, 12, 14, 16}, {32, 34,
36, 38} et {64, 66, 68, 70, 72}, produites sur les mandrins I, II et III respectivement.
Dans chaque famille le diamètre de branche augmente avec le numéro
de branche. Chaque branche a la même longueur et le même diamètre
final. Les branches d'embouchure de cornet sont basées sur cinq formes
qui sont numérotées, par diamètre croissant, R0, A0, G0,
T0 et K0. Les branches G2 et G4 sont également construites avec la même
forme que G0 mais avec des rayons légèrement plus grands. De
même
sont également produites les branches K2, K4, A2, R2 et T4. Noter que
les numéros sont utilisés pour marquer les branches et n’ont
aucune signification précise autre que la tendance générale
que, dans une famille, un numéro plus grand correspond à une
branche plus large.
Puisque tout fabricant est principalement intéressé à observer
la différence entre des branches « semblables » (qui sont
prévues pour être identiques) ou des branches « différentes » (conçues
pour produire un son différent), notre étude est centrée
sur la question de déterminer si le réflectomètre d'impulsion
est capable de ces mesures. Tout appareil de mesure doit être capable
de détecter de telles différences s'il doit servir à comparer
les instruments de musique et à aider les fabricants. La précision du
profil mesuré est également évaluée à l'extrémité des
branches, où elle peut être vérifiée avec un pied à coulisse.
2. La réflectométrie d'impulsion.
Le but de la réflectométrie d'impulsion est d'obtenir le rayon
interne d'un objet tubulaire. Ceci est fait en déterminant la réponse
d'impulsion d'entrée de l'objet, qui est alors analysée pour
déterminer
le profil interne de perce.
2.1. La réponse d'impulsion d'entrée.
La réponse d'impulsion d'entrée est la séquence de réflexions
qui serait obtenue si une impulsion acoustique étaient envoyée
dans l'objet. Par exemple, considérons un objet se composant de trois
sections cylindrique c1, c2 et c3, représenté sur la figure 1.
Quand une impulsion acoustique se propage dans un tel tube, elle sera partiellement
réfléchie et partiellement transmise à chacun des changements
de rayon (y compris l’extrémité ouverte) ; les réflexions
et les transmissions partielles à l'étape c1:c2 entre les cylindres
c1 et c2 sont montrées sur la figure 1. Ainsi la réponse d'impulsion
d'entrée sera une série de pics correspondant aux réflexions
aux étapes c1:c2, c2:c3… et également aux réflexions
multiples qui se produisent, par exemple, quand l'impulsion d'entrée
transmise par c1:c2 est réfléchie par c2:c3 et finalement retransmise
par c1:c2 vers la source. La forme de chacun des pics constituant la réponse
d'impulsion d'entrée sera légèrement différente
de l'impulsion en raison des pertes subies par l'impulsion au cours de sa propagation
dans l'objet.
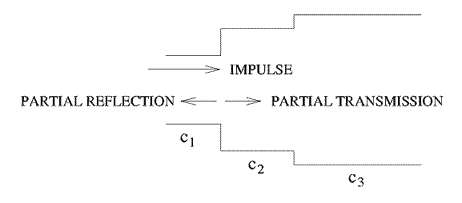
Figure 1. Un objet composé de trois cylindres
c1, c2 et c3.
On a représenté un signal d'impulsion entrant dans l'objet,
de même que
la réflexion partielle et la transmission partielle à c1:c2.
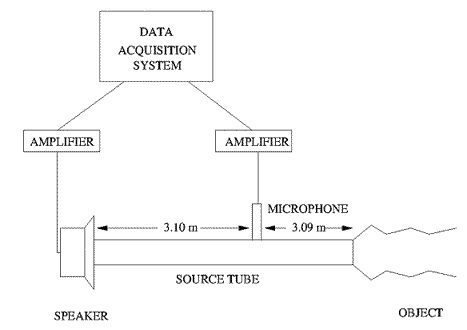
Figure
2. Diagramme schématique du réflectomètre
d'impulsion.
Il n'est pas possible de mesurer la réponse d'impulsion
d'entrée
directement puisqu'il est impossible de créer une impulsion acoustique
idéale. La figure 2 montre un diagramme schématique de l'appareil
utilisé pour obtenir la réponse d'impulsion d'entrée.
L'impulsion initiale est produite en envoyant une impulsion carrée d’une
durée de 80 µs au haut-parleur. L'impulsion acoustique résultante émise
par le haut-parleur se propage le long du tube source, passe devant le microphone
et entre dans l'objet. Les réflexions de l'objet se propagent en retour
le long du tube source et sont détectées par le microphone qui
est serti dans la paroi du tube source de sorte que la face avant du micro
affleure la paroi aussi précisément que possible. Le signal reçu
du micro est alors amplifié et échantillonné à 50
kilohertz. Ici 1024 échantillons du signal réfléchi sont
enregistrés donnant une série temporelle de réflexion
durant approximativement 20 ms. La longueur du tube source et la position du
microphone sont choisies pour s'assurer que seules les réflexions produites
par l'objet sont enregistrées et non pas l'impulsion d'entrée
ni les réflexions secondaires du haut-parleur. L'appareil est montré sur
la figure 3.

Figure 3. Le réflectomètre d'impulsion
En
utilisant la technique décrite ci-dessus, il est possible de mesurer
les réflexions de l'objet ; cependant, ce n'est pas la réponse
d'impulsion d'entrée parce que l'impulsion acoustique initiale n'est
pas une fonction d'impulsion. Pour calculer la fonction de réponse d'impulsion
d'entrée nous avons besoin de déconvoluer la réflexion
mesurée avec l'impulsion d'entrée. Ainsi la réponse d'impulsion
d'entrée est donnée par la transformée de Fourier inverse
de IIR(ω)
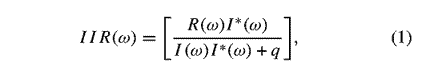
où R(ω) est la transformée
de Fourier des réflexions mesurées,
I(ω) est la transformée de Fourier de l'impulsion d'entrée
et q est un petit facteur de contrainte pour empêcher la division par
zéro. L'impulsion d'entrée a été mesurée
en enlevant l'objet et en le remplaçant par un bouchon rigide qui
termine le tube source et produit une réflexion parfaite de l'impulsion
d'entrée. Cela assure que toutes les pertes de signal dans le tube,
entre le microphone et l'objet ou le bouchon, sont prises en compte dans
la déconvolution. Le rapport signal/bruit a été amélioré en
prenant 1000 moyennes des deux signaux avant d'effectuer la déconvolution
et les mesures ont été effectuées dans une chambre sourde.
Enfin, il est important de s'assurer qu'il n'y a aucune composante continue
dans les signaux enregistrés ; celle-ci ne vient pas des effets acoustiques
mais de l'électronique entre le microphone et l'ordinateur. La valeur
de la composante continue impose une augmentation ou une diminution incorrecte
au rayon (puisqu'elle n'est pas présente dans le signal acoustique)
qui est ajoutée consécutivement à chaque point le long
de l'objet dans la reconstitution finale. Ainsi même une très
faible composante continue peut ajouter une erreur importante à la
mesure du rayon à l'extrémité éloignée
du tube. Pour obtenir la valeur de la composante continue additionnelle,
on insère un tube de 403 millimètres de long et de rayon constant
entre le tube source et l'objet. Le « tube DC » devient maintenant
une partie de l'objet à mesurer parce qu'il correspond aux 403 premiers
millimètres de la reconstitution. Avec le « tube DC » en
place la réponse d'impulsion d'entrée est calculée comme
précédemment avec l'équation (1). Maintenant, on sait
qu’aucune réflexion ne se produira pendant les premières
2l/c secondes, où l est la longueur du « tube DC » et
c la vitesse du son. La valeur moyenne de la réponse d'impulsion d'entrée
obtenue pendant cet intervalle de temps correspond à la valeur de
la composante continue. Cette valeur est alors soustraite du signal entier.
Ceci s'est avérée une méthode efficace pour enlever
le terme continu [7.11].
3. Reconstitution de la perce.
La réponse discrète d'impulsion d'entrée est une série
temporelle de réflexions en provenance de l'objet. Ces réflexions
se produisent toutes les fois qu'il y a une variation de l'impédance
due à une augmentation ou une diminution du rayon du tube. Les objets
considérés ont généralement un rayon qui varie
continûment. Afin d'évaluer la perce interne nous représentons
approximativement l'objet par une série de petits cylindres c1,
c2. . . , chacun de longueur cδt/2, où δt est l'échantillon
de temps. La section de chaque pas peut être calculée pourvu
que la section initiale de l'objet soit connue (ou puisse être mesurée).
Notons que la notation utilisée ici est semblable à la notation
présentée sur la figure 1 ; cependant, ici chaque cylindre
a la même longueur, l = cδt/2 et le rayon de chaque cylindre
est le rayon moyen de l'objet réel dans la longueur correspondante
l. Si un objet a un rayon constant sur plusieurs des cylindres-échantillon,
alors il n’y aura aucune réflexion à cet endroit. Néanmoins,
toutes les transitions entre les cylindres sont prises en compte séparément
dans l'algorithme de reconstitution. Le premier terme de la série
de réponse d'impulsion d'entrée correspond à la réflexion
de l'impulsion à la frontière entre les premier et deuxième
cylindres. Ainsi on peut obtenir la variation d'impédance, et par
conséquent la variation du rayon à c1:c2. Ceci peut être
répété en notant que les termes suivants de la série
se composent des réflexions primaires et des réflexions multiples.
Le taux d'échantillon utilisé partout était de 50 kilohertz.
L'augmentation du taux d'échantillon à 100 kilohertz augmente
la résolution des points le long de l'axe de l'objet. A part cela,
on n’observe aucune augmentation discernable de la précision
en diminuant la longueur des cylindres-échantillon. Il n'y a également
aucune augmentation de la largeur de bande puisqu'il n'y a aucun signal mesurable
au-dessus de 25 kilohertz.
Pour obtenir une bonne précision, il faut tenir compte des pertes visqueuses
encourues par le signal à l'intérieur de l'objet. Celles-ci peuvent être
significatives pour le rayon des objets que nous considérons et sont
représentées par Keefe [17] comme fonction du rayon et de la
fréquence. Ainsi dans chaque cylindre-échantillon les différentes
fréquences composant l'impulsion seront amorties à des taux différents.
Les changements résultants de forme et d'amplitude de l'impulsion sont
pris en compte par un filtre de pertes. On peut trouver dans [13.14] une présentation
détaillée de l'algorithme du filtre de pertes.
Le tube DC a été relié à la branche d'embouchure
et au tube source à l'aide des coupleurs spécialement conçus,
comme représenté sur la figure 4. Le coupleur joignant le tube
source et le tube DC est conçu pour maintenir le rayon approximativement
constant. Il y a une petite discontinuité de rayon à l'intérieur
du coupleur joignant le tube DC à la branche d'embouchure. Différents
coupleurs ont été construits de façon que le deuxième
rayon interne du coupleur s’aligne approximativement sur le rayon interne
de la branche d'embouchure à mesurer. Ainsi la discontinuité peut être
une augmentation ou une diminution du rayon selon la branche d'embouchure.
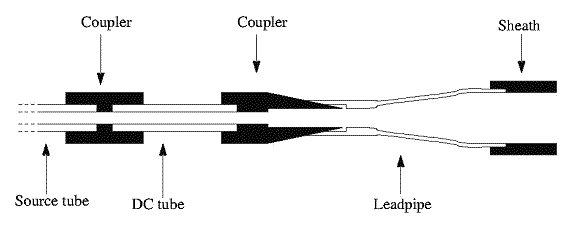
Figure 4. Diagramme schématique (sans échelle)
montrant comment le tube source, le tube DC,
la branche
d'embouchure (leadpipe) et la gaine (sheath) sont couplés.
Il est bien connu qu'il se produit
une série d'ondulation dans une
reconstitution toutes les fois qu'il y a une grande discontinuité dans
le rayon de l'objet, y compris l'extrémité ouverte d'une branche
[7.11]. C'est le phénomène de Gibbs, qui surgit en raison de
la largeur de bande finie des réflexions échantillonnées.
Pour améliorer la reconstitution près de l'extrémité ouverte
de la branche d'embouchure, une gaine cylindrique a été enfilée
sur l'extrémité ouverte. C'est comme le tube de la trompette
qui prolonge normalement la branche d'embouchure et cela a pour effet d'enlever
l'ondulation de la reconstitution à la fin de la branche d'embouchure.
Cette gaine est également montrée sur la figure 4.
4. Résultats.
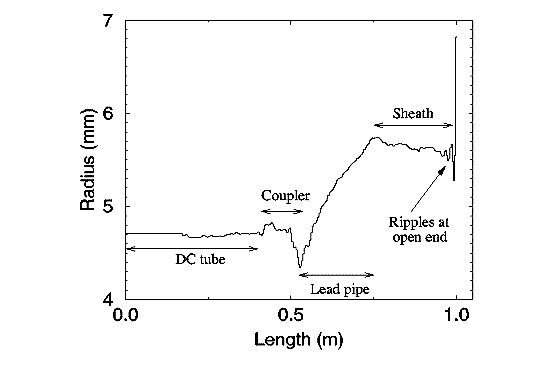
Figure 5. Une reconstitution typique de la branche 10.
La position du tube DC, du coupleur,
de la branche d'embouchure et de la gaine sont indiquées sur le graphique.
Sont indiquées aussi les ondulations qui se produisent autour d’une
importante
discontinuité ou d’une extrémité ouverte, ici l’extrémité ouverte
de la gaine.
La figure 5 montre une reconstitution typique de la branche
10, dans laquelle les différentes parties de la reconstitution sont
identifiées.
La section initiale est le tube DC qui devrait avoir un rayon fixe. La première
partie du tube DC (approximativement 16,5 centimètres, correspondant à 1
ms du signal échantillonné) est fixée au rayon connu du
tube dans l'algorithme de reconstitution. Ceci enlève toute pic
numérique anormale dans la partie initiale du signal déconvolué.
La deuxième partie de la reconstitution du tube DC est calculée à partir
des réflexions échantillonnées. Ici nous voyons une petite
variation du rayon mesuré, très inférieure à 0,1
millimètre. La deuxième section de la reconstitution est le coupleur
utilisé pour relier le tube DC à la branche d'embouchure. Il
est conçu pour s’enfiler sur le tube DC de sorte que la discontinuité du
rayon interne soit minimale. Sur la figure 5 on voit qu’elle est d’environ
0,1 millimètre. On voit clairement aussi la petite discontinuité interne
dans le rayon du coupleur. Dans la partie initiale de la branche d'embouchure
il y a une partie conique qui reçoit la queue de l'embouchure de trompette.
A l'extrémité de ce récepteur, il y a diminution du rayon
de la branche (pour assurer la continuité du rayon entre l’intérieur
de la queue d’embouchure et la branche, N.d.T.). Sur le réflectomètre,
le coupleur est inséré dans la branche de la même manière
qu’une embouchure ; il y a donc un chevauchement entre le coupleur et
le début de la branche d'embouchure et ainsi cette partie initiale de
la branche n'est pas mesurée. La reconstitution de la branche commence
juste avant la discontinuité du rayon à l'extrémité du
récepteur d'embouchure. La variation du rayon de la branche d'embouchure
depuis cette discontinuité jusqu’à l'extrémité est
d’environ 1,5 millimètres, augmentant d'une façon continue
sur la longueur de la branche. Enfin nous voyons la gaine à la fin de
la branche d'embouchure. On observe l'ondulation sur la reconstitution à l'extrémité ouverte
de la gaine, et non à l’extrémité de la branche
d'embouchure.
4.1. Reproductibilité et précision
de la mesure.
En comparant la reconstitution d'un certain nombre de branches, pour observer
la différence entre les branches, ou pour comparer un certain nombre
de branches qui sont prévues pour être identiques, il est essentiel
de connaître la précision des mesures de sorte que nous puissions
déterminer si les différences dans la reconstitution correspondent à de
vraies différences dans les branches ou aux incertitudes dans la technique
de mesure. Un type d'incertitude quel est présent dans toute reconstitution
est une incertitude systématique qui se produit dans chaque mesure. Tandis
qu'il est souhaitable de pouvoir mesurer le rayon réel d'un objet avec
un degré élevé de précision, il convient de noter qu'on
peut encore observer des différences entre les branches (ce qui est notre
premier objectif ici) en dépit de toutes les incertitudes systématiques.
Il est donc plus important ici de considérer la reproductibilité et
la fiabilité des mesures ; la précision absolue des mesures de rayon
sera traitée brièvement dans le paragraphe 4.5.
La reproductibilité des mesures a été étudiée
de deux manières. La méthode 1 consistait à faire dix mesures
des réflexions de l'objet
sans enlever la branche ni toucher l'appareil d'aucune façon.
La méthode
2 consistait à prendre dix mesures séparées à différentes
heures et différents jours, cet essai étant plus représentatif
des conditions dans lesquelles le réflectomètre est susceptible
d'être utilisé dans un atelier d'instruments de musique.
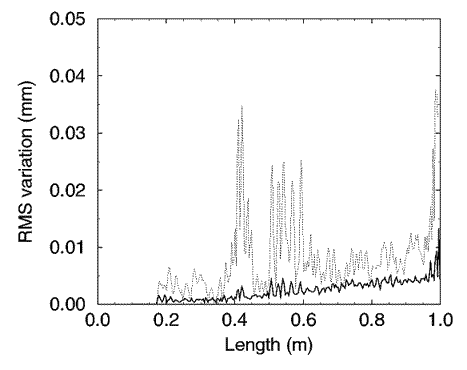
Figure 6. RMS des variations entre des reconstitutions
répétées de la branche 10.
Les
reconstitutions ont été répétées
en utilisant la méthode 1 (courbe pleine)
et la méthode 2 (courbe en pointillés).
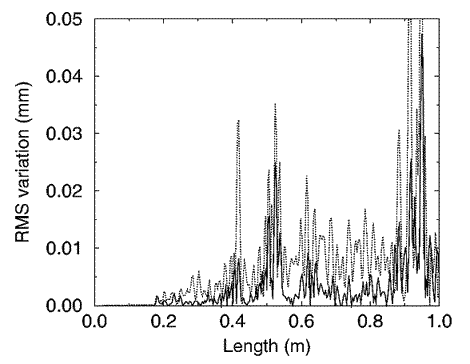
Figure 7. Moyenne quadratique (RMS) des variations entre les
reconstitutions répétées
de la branche G0.
Les reconstitutions ont été répétées
en utilisant la méthode 1 (courbe pleine) et
la méthode 2 (courbe pointillée).
Les méthodes 1 et 2 ont été utilisées
pour examiner la reproductibilité de la technique à l'aide des
branches 10, 38 et G0. La moyenne quadratique (désignée par
RMS = root mean square) de ces variations a été calculée
et est montrée sur les figures 6 et 7 pour les branches 10 et
G0 respectivement. Les résultats pour la méthode 1, correspondant à dix
mesures, sont représentés par la courbe
pleine et les résultats pour la méthode 2, correspondant à six
des dix mesures qui ont été choisies parce qu'elles ont été faites
à des températures semblables, sont représentées
par la courbe en pointillés. Sur la figure 5 nous pouvons
voir qu'il y a des discontinuité au voisinage de 0,4 et
0,5 m de l'origine de l'objet (dans le coupleur) et que la branche d'embouchure
de trompette se trouve entre environ 0,5 et 0,75 m. Une branche
d'embouchure de cornet fait environ de 0,5 à 0,9 m de long. Il
y a un certain nombre de caractéristiques générales
sur les figures 6 et 7 qui ont été également
observées
pour la branche 38. Premièrement, il y a un certain nombre de pics à approximativement
0,4 et 0,5 m correspondant aux discontinuités de diamètre dans
le coupleur et à environ
1,0 m dans la figure 6 et 0,9 m dans la figure 7 correspondant respectivement à l'extrémité ouverte
de la gaine et à l'extrémité de la branche d'embouchure
de cornet. Les pics observées pour la méthode 2 sont dus aux
différences
de température entre les mesures, et aux différences entre
la longueur du coupleur qui a été inséré dans la
branche (qu'on voit varier jusqu'à 2 millimètres).
Puisque la vitesse du son est une fonction de la température, le nombre
de points de mesure et leur séparation sera différent
pour des reconstitutions faites
à des temperatures* différentes.
Sur la figure 7 il y a des pics à 0,4
et 0,5 m pour la méthode 1 suggérant qu'il a pu y avoir un
petit changement de température pendant la demi-heure prise pour obtenir
les mesures. En dehors des pics, la moyenne quadratique
des variations est en général d'environ 0,01 millimètre
dans la région
des branches et généralement pas supérieure à 0,02
millimètre.
Ceci suggère que le réflectomètre d'impulsion
devrait pouvoir distinguer les branches pourvu qu'elles diffèrent
de plus de 0,03 millimètre de rayon environ. On peut s'attendre ce
que les variations autour des zones de discontinuité du rayon aient des
niveaux de reproductibilité similaires aux autres
régions
dans des conditions idéales de contrôle de la température.
* Noter que le problème se pose ici en raison
de la façon dont les résultats sont comparés. Normalement
la vitesse du son est prise en compte dans l'algorithme en changeant
la distance entre les points de mesure.
4.2. Reconstitution de branches d'embouchure de
trompette.
La figure 8 présente des reconstitutions de branches d'embouchure de trompette,
pour les deux mandrins I et II. Trois exemplaires de la branche 10 (désignés
par 10a, 10b et 10c) et quatre de la branche 38 (branches
38a,
38b, 38c et 38d) ont été reconstitués et sont également
présentés sur la figure 8. Les exemplaires des branches
sont prévus
pour être identiques, mais ils ne peuvent pas l'être
totalement. Les graphiques ne portent que sur la branche d'embouchure, et
l'axe de longueur a été gradué de
telle sorte que zéro
corresponde au début de la branche. Dans certaines des branches où la
discontinuité initiale est plus importante, on observe une certaine
ondulation dans la reconstitution (voir par exemple la branche 10). Cette ondulation
peut perturber un peu les mesures, particulièrement
près
de la discontinuité, et peut empêcher de détecter de petites
différences. Dans la section centrale, entre une éventuelle ondulation
initiale et la convergence à l'extrémité des
branches, les différences entre les différentes tailles de branches
sont clairement onservables dans chaque famille. En outre la
différence
entre les exemplaires d'un même modèle de branche est beaucoup
plus petite que la différence
entre des modèles différents (branches portant un numéro
différent).
Ainsi, si on avait affaire à une branche inconnue, il devrait être
possible de déterminer quelle branche c'est.
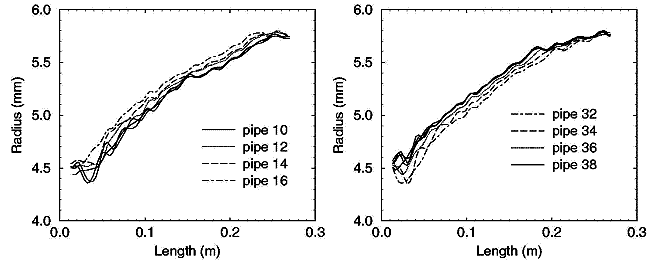
Figure 8. Reconstitution des quatre branches des familles
de mandrins I et II : on montre ici trois exemplaires de la branche 10 et quatre
de la branche 38.
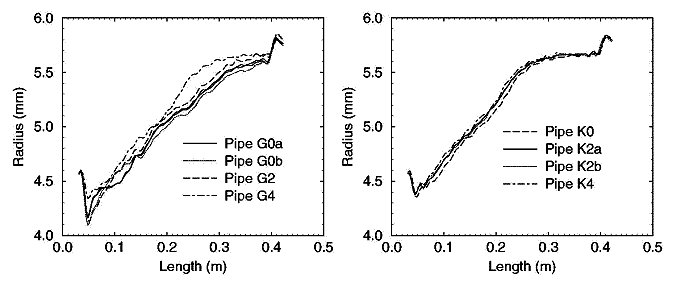
Figure 9. Reconstitution des familles G et K des branches
d'embouchure de cornet. On montre la reconstitution de deux exemplaires de
la G0 et deux de la K2.
4.3. Reconstitution de branches d'embouchure
de cornet.
Portons maintenant notre attention sur les reconstitutions de branches
d'embouchure de cornet. La figure 9 montre des reconstitutions des branches
de types G et K. Ces deux familles contiennent trois branches marquées
0, 2 et 4 à mesure
que leur rayon augmente. Nous avons également étudié la
reproduction G0 et les branches K2. On voit clairement sur la
figure 9 que le rayon moyen de la famille G est plus petit que celui de
la famille de K, et que la gamme des rayons dans la famille K est moins
étendue que dans famille G. La Figure 9 montre seulement une
petite différence
entre la branche K0 et K4, en général environ 0,1 millimètre.
On voit que les profils des deux exemplaires de la K2 s'intercalent entre ceux
des K0 et K4 sur l'ensemble de leur longueur, et que la parenté entre
les deux branches K2 est bien plus grande que l'accord entre n'importe laquelle
des autres courbes. Ceci montre le degré élevé de précision
atteint dans la fabrication des deux branches K2 où la courbure des
branches n'introduit que peu de variations. La figure 9 montre également
la croissance du rayon des branches G0 à G4. C'est évident
partout excepté près de l'origine où la branche
G2 semble plus petite que les deux branches G0. Comme c'est proche
de la discontinuité initiale et que les différences sont faibles
il est difficile de dire
si c'est dû à une petite ondulation sur la reconstitution. Il
y a également
une différence significative entre les deux branches G0. En beaucoup
d'endroits la différence entre les deux branches G0 est comparable à la
différence entre la branche G0 la plus large et la branche G2,
et dans quelques endroits elle est même supérieure. On voit aussi
que G0b est plus étroite que G0a sur la majeure partie
de sa longueur, mais que près de l'embouchure elle est plus large.
Noter que la figure 9 présente deux mesures répétées
de la branche G0a, et elles sont en bon accord. Les mesures répétées
de G0b ont montré de même une bonne concordance avec la reconstitution
qui est représentée ici. On ne sait pas pourquoi la différences
entre les branches G0a et G0b est supérieure à la différence
entre des esemplaires d'autres branches. Le
fabricant s'attend à ce
que les branches de cornet présentent une plus grande dispersion
de caractéristiques due à leur
forme incurvée ; ceci a pu expliquer la déviation. Il est également
possible qu'une des branches ait été endommagée d'une
manière quelconque, pendant sa fabrication, son transport
ou pendant sa mesure.
Examinons maintenant la gamme complète des branches de cornet à travers
les cinq branches R0, A0, G0, K0 et T0 représentées sur
la figure 10. Le fabricant [16] indique que les branches devraient avoir un
rayon croissant du plus petit (R0) au plus grand (T0) en passant par A0, G0
et K0. La figure
10 présente les deux branches G0 pour montrer
comment elles s'insèrent entre les différentes familles.
Clairement les branches ont bien le rayon croissant indiqué par
le fabricant, et les branches sont reconnaissables excepté la plus petite
branche, la R0, qui produit une grande quantité d'ondulations.
La discontinuité (due au récepteur d'embouchure, NdT)
à l'entrée de cette branche est plus grande que dans chacune
des autres. L'amplitude de l'ondulation est, à son
maximum, d'environ 0,3 millimètre, ce qui serait acceptable dans beaucoup
d'applications ; cependant, ici elle rend impossible de comparer la branche
R0 aux autres, au moins pour la première
moitié de
la branche. Les deux branches G0 se trouvent entre la A0 et la
T0 sur la majeure partie de leur longueur, excepté une partie
comprise entre 0,08 et 0,15 m où G0a devient sensiblement plus petite
que A0. Ceci suggère
que G0b pourrait être la branche correcte et G0a
celle qui a été endommagée,
bien que la preuve n'en soit pas constituée ; il faudrait mesurer un
autre exemplaire de G0 pour le confirmer.
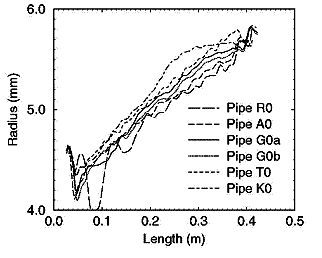
Figure
10. Reconstitution des branches d'embouchure
de cornet R0, A0, G0, T0 et K0.
On montre les
deux exemplaires de la branche G0.
4.4. Différences entre exemplaires d'un
même modèle
de branche.
Les exemplaires de branches que nous avons eu à notre disposition étaient
10a, 10b, 10c ; 38a, 38b, 38c, 38d ; G0a, G0b et K2a, K2b. On a mesuré
plusieurs fois chacune de ces branches et étudié les différences
entre exemplaires, par exemple 10a-10b.
La figure 11 montre ces différences pour les branches 38 et K2
et deux de ces différences pour la
branche G0. Les résultats présentés pour
les branches 38 et K2 sont typiques des autres résultats obtenus pour
ces branches et pour les résultats
obtenus pour la branche 10. La différence entre exemplaires d'un modèle
de branche n'est généralement pas supérieure à la différence
observée
entre des mesures répétées d'une même branche.
Ainsi la dispersion entre répliques d'une même branche
est trop petite pour que le réflectomètre la détecte.
Les deux comparaisons répétées des branches G0a
et G0b montrent une différence notable entre branches
qui est distincte de la dispersion des mesures répétées
d'une même branche. Nous pouvons donc dire avec certitude qu'il y a
une différence
observable entre les deux branches G0, bien que la différence
ne soit jamais supérieure à 0,12 millimètre.
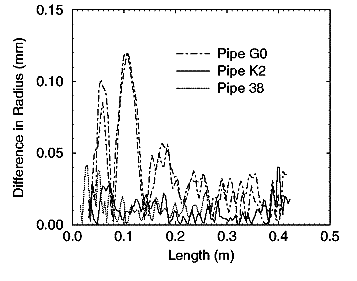
Figure 11. Différences entre
les reconstitutions des branches G0, K2 et 38.
4.5. Précision des mesures.
Dans les paragraphes précédents nous nous somme plus préoccupés
de comparer la forme d'une série de branches plutôt que d'obtenir
une mesure exacte de leur rayon. Pour étudier la précision des mesures
de rayon faites par le réflectomètre d'impulsion, on a étudié
les rayons des extrémités obtenus à partir
de chacune des reconstitutions de branche d'embouchure de trompette.
Les rayons ont été arrondis au 0,01 millimètre
le plus proche. Les résultats sont présentés sur la figure 12
qui montre l'occurrence de chaque rayon. Le graphique pour l'ensemble des
branches de trompette a deux pics distincts de part et d'autre du rayon moyen
de 5,755 millimètres. La courbe pour le mandrin I présente un pic à 5,75
millimètres tandis que les mandrin II et III présentent des
pics à 5,77 millimètres, ce qui explique le double
pic observé dans la courbe pour l'ensemble des branches. La dispersion
des résultats est de 0,1 millimètre, tous les résultats
étant compris entre 5,7 et 5,8 millimètres. La courbe pour la
branche 10a fait une pointe à 5,73 millimètres et a une dispersion
telle que plus de 75 % des résultats pour le rayon final sont
dans une fourchette de 0,03 millimètre ; c'est conforme aux résultats
de moyenne quadratique présentés ci-dessus et à l'affirmation
que des différences
entre branches aussi petites que 0,03 millimètre peuvent être
détectées.
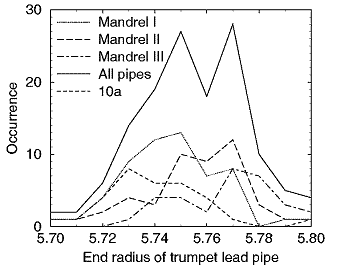
Figure 12. Occurrence de chaque rayon d'extrémité (arrondi au
0,01 millimètre le plus proche)
pour chacune des reconstitutions de branche
d'embouchure de trompette.
Les résultats sont présentés en cinq
groupes correspondant à l'ensemble
des branches de trompette, toutes les branches
construites avec chacun
des mandrins I, II et III, et à
toutes les reconstitutions de la seule branche 10a.
La figure 12, cependant, ne met en lumière que les différences
; elle ne répond pas à la question de la précision d'une mesure du rayon d'extrémité de
la branche obtenue par le réflectomètre. Le rayon d'extrémité d'une
branche 10a a été mesuré à l'aide d'un pied à coulisse
qui donne 5,75 ± 0,025 millimètres. Les 32 reconstitutions
de la branche 10a, représentées sur la figure 12, ont une valeur
moyenne de 5,742 millimètres pour le rayon d'extrémité,
avec un écart
type de 0,020 millimètre, et aucune des reconstitutions n'a un rayon
d'extrémité en dehors de la plage 5.7-5.8 millimètres.
Par conséquent, on peut penser que
l'incertitude sur la mesure à l'extrémité de la branche d'embouchure de trompette
n'est pas supérieure à ± 0,05 millimètre.
Comme prévu, c'est
plus grand que la variation observée entre les reconstitutions d'une
même branche (~0,03 millimètre) et que l'incertitude avec laquelle
le rayon initial du tube DC peut être mesuré (±0,025 millimètre).
Bien que supérieure à l'incertitude obtenue
avec un pied à coulisse, cette incertitude est relativement
petite et suggère que le réflectomètre soit non seulement
utile pour observer de petites différences entre les objets, mais également
pour donner une mesure précise du rayon interne. On
s'attend à ce que la valeur de ±0,05 millimètre pour l'incertitude
dans une mesure augmente avec la longueur et la taille de l'objet à
mesurer. Il faut également noter que le réflectomètre
mesure en fait la section d'un objet et donnera donc une valeur
moyenne du rayon si la section transversale n'est pas circulaire. En outre,
il n'est clairement pas possible d'obtenir des mesures avec cette précision
dans les régions de la reconstitution où apparaissent des ondulations.
5. Discussion.
D'une façon générale, ces résultats ont prouvé que
les différentes
branches d'embouchure peuvent être distinguées les unes des autres à l'aide
du réflectomètre d'impulsion. Cependant, dans quelques reconstitutions
l'ondulation qui peut se produire à toute discontinuité de rayon dans
la branche peut masquer le rayon réel de la branche. Dans la plupart
des cas l'ondulation n'est pas assez grande pour poser un problème significatif
; cependant, trois des branches ont produit une quantité substantielle
d'ondulations par rapport aux différences de rayon que nous mesurons.
Ce sont les trois plus petites branches où la discontinuité
est la plus grande : la branche 10 (voir la figure 8), la branche R0 (voir
la figure 10) et la branche R2 (non représentée). Sur la figure
8 l'ondulation sur la reconstitution de la branche 10 est évidente sur
la majeure partie de la reconstitution ; c'est seulement dans les 10 premiers
centimètres que le niveau de l'ondulation est inacceptable puisque
nous ne pouvons plus séparer la branche 10 des branches 12 et 14.
L'ondulation sur la branche R0 sur la figure 10 est plus génante que sur la
branche 10 et elle est inacceptable parce qu'elle rend presque la première
moitié de
la reconstitution inutilisable. Excepté ces trois branches, cependant,
l'ondulation n'est pas un problème réel. Néanmoins, il
serait utile de résoudre le problème de l'ondulation.
Une approche possible est d'utiliser des techniques de post-traitement pour
introduire des retards de temps partiels de façon que l'écart entre deux cylindres-échatillon
coïncide avec l'écart réel.
Il faudrait un travail de recherche complémentaire pour valider cette approche,
à la fois en termes de réduction des ondulations et de temps de calcul.
6. Conclusion.
Un certain nombre de branches d'embouchure de trompette et de cornet ont été étudiées
en utilisant la réflectométrie d'impulsion. En changeant de
branche d'embouchure un instrumentiste peut changer significativement les
caractéristiques musicales de jeu de l'instrument, mais les différences
entre les branches sont faibles : typiquement le rayon différera
de moins de 0,1 millimètre entre des branches semblables. En comparant
des reconstitutions de ces branches d'embouchure nous avons examiné la
capacité du réflectomètre à les distinguer entre elles.
Le réflectomètre
peut typiquement détecter des différences de rayon supérieures
à 0,03 millimètre. Puisque toutes les
branches qui sont nominalement de la même taille ne sont pas identiques,
les différences
entre des exemplaires d'une même branches ont été également étudiées.
Dans la plupart des cas les différences étaient inférieures à
0,03 millimètre et au-dessous de la résolution du
réflectomètre.
Dans un cas on a observé des différences discernables entre deux
exemplaires d'une branche d'embouchure de cornet. Ces différences
pourraient être apparues pendant la fabrication des branches, en particulier
dans le recourbement de la branche d'embouchure de cornet, ou bien elles pourraient être
dues à des dommages postérieurs. La différence entre les
exemplaires d'une branches était
en général plus petite que les différences observées
entre les branches voisines qui peuvent facilement être
identifiées
par le réflectomètre. La précision des mesures obtenues à partir
du réflectomètre a été également considérée
brièvement. À l'extrémité de la branche l'incertitude
tirée d'une reconstitution s'est avérée ±0,05 millimètre.
C'est légèrement moins précis que la mesure par un pied
à coulisse
; cependant, le réflectomètre a l'avantage de pouvoir faire des
mesures dans les endroits inaccessibles. On a évoqué brièvement les problèmes
qui restent à résoudre en réflectométrie ; la difficulté principale
observée ici est l'ondulation qui apparaît dans une reconstitution
près d'une discontinuité de rayon.
De façon générale, le réflectomètre s'est
avéré capable de détecter de petites différences
entre branches d'embouchure qui produisent des différences de caractéristiques
musicales des trompettes et cornets faibles mais audibles.
Ainsi nous concluons que le réflectomètre est un outil utile
pour étudier les instruments de musique tubulaires et également
pour diagnostiquer et localiser de façon précise des défauts
pendant la fabrication des instrument.
Remerciements.
Ce travail a été soutenu par le Conseil de la recherche en
technologie et sciences physiques, R-U.
Références :
[1] Kausel W 2001 "Bore reconstruction from measured acoustic
input impedance; equipment, signal processing, algorithms
and prerequisites" ISMA2001: Proc. Int. Symp. on Musical
Acoustics (Perugia, 2001) vol 2 pp 373-8 (version augmentée de son article
de 1999 "Optimisation
informatique des cuivres" NdT)
[2] Ware J A et Aki K 1969 "Continuous
and discrete inverse
scattering problems in a stratified elastic medium: I. Planes
at normal incidence" J. Acoust. Soc. Am. 45 911-21
[3] Jackson A C, Butler J
P, Millet E J, Hoppin F G et
Dawson S V 1977 "Airway geometry by analysis of acoustic
pulse response measurements" J. Appl. Physiol. 43
523-36
[4] Fredberg J J, Wohl M E B, Glass G M et Dorkin H L 1980 "Airway area by acoustic reflections measured at the mouth" J.
Appl. Physiol. 48 749-58
[5] Brooks L J, Castile R G, Glass G M, Griscom
N T,
Wohl M E B et Fredberg J J 1984 "Reproducibility and
accuracy of airway area by acoustic reflection" J. Appl.
Physiol. 47 777-87
[6] Smith R A 1988 "Its
all in the bore!" J. Int. Trumpet
Guild 12
42-5 (traduction française)
[7] Sharp D B et Campbell D M 1997 "Leak detection in pipes
using acoustic pulse reflectometry" Acustica 83 560-6
[8] Campbell D M et MacGillivray
T 1998 "Reconstruction of the
carnyx" ISMA98: Proc. Int. Symp. on Musical Acoustics
(Leavenworth, WA, 1998) pp 147-52
[9] Sharp D B, MacGillivray T J, Ring W,
Buick J M rt
Campbell D M 1998 "Acoustical comparison of bassoon
crooks" ISMA98: Proc. Int. Symp. on Musical Acoustics
(Leavenworth, WA, 1998) pp 209-14
[10] Sharp D B et Buick J M 1999 "Measurement
of musical wind
instruments using acoustic pulse reflectometry". Proc.
Institute of Acoustics (London) vol 21 pp 191-8
[11] Sharp D B 1998 "Increasing
the length of tubular objects that
can be measured using acoustic pulse reflectometry" Meas.
Sci. Technol. 9 1469-79
[12] MacGillivray T J et Greated C A 1999 "Acoustic
pulse
reflectometry for the measurement of tubular structures" Acustica 85 s217
[13] Rosenhouse G, Amir N et Shimony U 1995 eA discrete model
for tubular acoustic systems with varying cross section—the
direct and inverse problems. Part 1: theory" Acustica 81
450-62
[14] Rosenhouse G, Amir N et Shimony U 1995 "A discrete model
for tubular acoustic systems with varying cross section—the
direct and inverse problems. Part 2: experiments" Acustica
81 463-74
[15] Smith R A et Daniell G J 1976 "Systematic
approach to the correction of intonation in wind instruments" Nature
262 761-5 (traduction française)
[16] http://www.smithwatkins.com
[17] Keefe D H 1984 "Acoustical wave propagation
in cylindrical
ducts: transmission line parameter approximations for
isothermal and non isothermal boundary conditions" J. Acoust. Soc. Am.
75 58-62
Traduit en janvier 2004 par Joël
Eymard pour le site web "Tout
sur la trompette"