Original version in English

Une approche systématique de la correction de justesse des instruments à vent

Richard A. Smith
Boosey and Hawkes Ltd, Edgware, Middlesex, UK et Department of Physics, Southampton University
Geoffrey J. Daniell
Department of Physics, Southampton University, Southampton SO9 5NH, UK

Les instruments de musique ont évolué au cours des siècles en grande partie par essais et correction d’erreurs. Malgré les recherches scientifiques, de nombreux facteurs indéterminés affectent de façon critique le jeu des instruments, et on doit encore recourir à des méthodes empiriques de conception. Quelques caractéristiques, cependant, sont facilement susceptibles d’un traitement quantitatif, et nous présentons ici les résultats de quelques calculs et expériences sur l’amélioration de la justesse et du timbre de la trompette.
Tous les cuivres ont des insuffisances acoustiques et mécaniques que la plupart des instrumentistes compensent automatiquement1. Pour l'auditeur moyen, un instrument peut jouer parfaitement juste mais ceci résulte en grande partie de la compétence de l'instrumentiste qui peut être capable de corriger une note de ± ½ ton avec les lèvres, habituellement aux dépens de la qualité du son. De même, la justesse de jeu des instrumentistes inexpérimentés tend à être affectée davantage par les défauts de leurs instruments.
La fréquence d'une note produite par une trompette est déterminée par une interaction complexe entre la colonne d'air vibrant dans l'instrument et les lèvres de l'instrumentiste. Elle est également affectée par rétroaction acoustique aux oreilles de l'instrumentiste, et on observe des différences de plus de 10 cents (1 cent = 0,01 demi-ton tempéré) quand différents instrumentistes utilisent le même instrument. La fréquence jouée est cependant toujours très proche d'une fréquence de résonance de la colonne d'air de la trompette.
Plusieurs auteurs2-7 ont reconnu la nécessité d'éliminer d'abord la contribution de l'instrumentiste individuel à la justesse, mais aucune méthode satisfaisante d'excitation artificielle n'a été encore décrite. Nous avons utilisé une variante de la méthode décrite à l'origine par Webster3 pour mesurer les fréquences de résonance de la colonne d'air dans la trompette. L'appareil (fig. 1) fonctionne sur la gamme de fréquence Ut2 (65 hertz) à Si7 (3951 hertz) (Ut4 = Ut médian) et inclut un dispositif de repérage et de calage automatique sur l'emplacement des pics de résonance. Il offre un affichage numérique et un enregistrement imprimé de l'amplitude et de la justesse de chaque résonance (en cents) par rapport à la gamme tempérée.

Fig. 1 L'appareil conçu pour localiser automatiquement et
détecter les résonances d'un instrument à vent. L'affichage numérique
indique la justesse et l'amplitude des résonances
.

On a constaté que la fréquence de chaque résonance d'un instrument correspondait étroitement à la moyenne des fréquences produites pour cette note par un certain nombre d'instrumentistes, de sorte que les observations faites avec cet appareil peuvent donc être utilisées comme base de la mesure quantitative de la justesse de l'instrument.

Résonances et couleur de son
Les fréquences de résonance sont principalement déterminées par la forme de la perce de la trompette, et l'évolution a produit une forme de perce produisant des résonances assez proches des notes correspondantes de la gamme tempérée. Malheureusement la justesse n'est pas le seul critère à considérer quand on fixe les résonances comme le montre l'exemple suivant.
La figure 2 montre les 10 premières résonances du tube avec leur correspondance en fréquences de la gamme tempérée .

Fig. 2 Les 10 premières résonances d'une trompette en Sib avec leur fréquence dans la gamme tempérée. *Non utilisée normalement.

Résonance	1*	2	3	4	5	6	7*	8	9	10
Note	Sib2	Sib3	Fa4	Sib4	Ré5	Fa5	Lab5	Sib5	Ut6	Ré6
Fréquence (Hz)	116,54	233,08	349,23	466,16	587,33	698,46	830,61	932,33	1046,5	1174,7

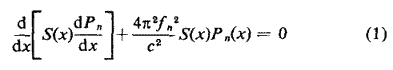
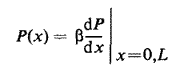
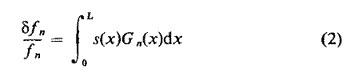
où

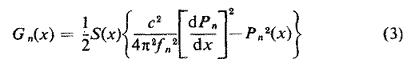
En la dérivant, il faut mettre dS à zéro aux deux extrémités de l'instrument de sorte que les conditions aux limites soient inchangées. Les valeurs de Pn(x) utilisées ci-dessus sont supposées normalisées, de sorte que

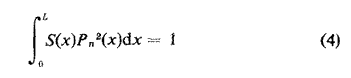
Ceci implique que la dimension de P soit L-3/2, et non celle d'une pression. Ont peut tirer une expression alternative de Gn(x) en partant de l'équation (1)

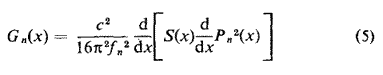
Nous voulons prescrire dfn et calculer dS(x). Il est clair que la solution n'est pas unique, et nous chercherons les variations les plus "lissées" de la perce qui produisent les décalages de fréquences requis. Il n'est pas pratique de faire des modifications sur l'ensemble de l'instrument, à cause des pistons et de la coulisse d'accord, et nous les restreindrons à la zone allant de x = 0 à x = l.
Pour éviter toute discontinuité de la perce, il faut dS(0) = 0 and dS(l) = 0.
Une mesure convenable du lissage est la moyenne quadratique de la dérivée

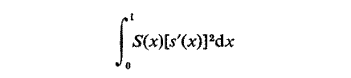
que nous allons minimiser, sous la contrainte que s(x) produise les décalages de fréquence requis en utilisant la méthode des multiplicateurs de Lagrange, ce qui conduit à minimiser

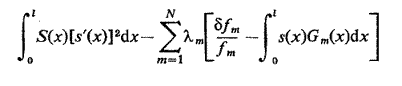
L'équation d'Euler de ce problême est

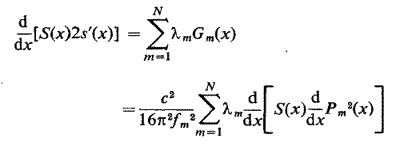
Après deux intégrations, nous obtenons

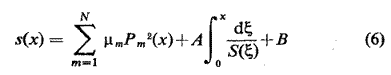
A et B sont des constantes d'intégration arbitraires et peuvent être choisies pour avoir dS(0) = 0 et dS(l) = 0, et mm est un multiple de lm.
En substituant dans (2) on obtient N équations linéaires qui, avec les conditions surdS, determinent les N+2 constantes mm , A, B. L'équation (6) donne alors les variations de perce requises.
Le lecteur peut se demander pourquoi nous avons utilisé la perturbation la plus "lissée" plutôt que la plus petite. Si nous définissons

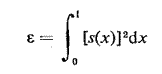
et cherchons la fonction s(x) qui le minimise et produit les décalages de fréquences requis, nous obtenons

Cette fonction ne peut toutefois être utilisée pour résoudre notre problème puisqu'elle n'assure pas que dS(0) = 0 et dS(l) = 0.

Les fonctions propres des ondes stationnaires
On a besoin des fonctions Pn(x) pour effectuer les calculs du paragraphe précédent. Bien qu'il soit possible, en principe, de les calculer à partir de la section de la trompette, il est assurément plus facile de les mesurer.
Dans une onde stationnaire, quand l'amortissement est très faible, les oscillations ont la même phase en tous points entre des nœuds adjacents, et la phase change de p en franchissant chaque nœud. Ce résultat n'est pas exact si on tient compte de l'amortissement, mais comme nous avons négligé l'amortissement, même dans l'équation (1), il n'y a aucun intérêt observer la phase des oscillations de pression, et nous supposerons que la phase est 0 ou p. La fonction Pn(x) est donc donnée par l'amplitude de pression observée entre les paires alternatives de nœuds moins la pression observée dans les intervalles.
On a également besoin de la dérivée dPn/dx. En raison des dangers bien connus de la différentiation numérique nous l'obtenons en intégrant l'équation (1) ce qui donne

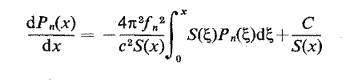
La valeur de la constante d'intégration C est obtenue en intégrant de nouveau, introduisant ainsi une autre constante, et on obtient les deux constantes en appliquant les équations à deux valeurs particulières de x.

Influence de la longueur de tube où sont appliquées les modifications
On peut tirer un résulat intéressant sur la moyenne quadratique des perturbations, qui peut être évaluée avec l'équation (7). Elle peut être dérivée par rapport à l, sachant que les valeurs de m dependent de l. Les dérivées de m peuvent être éliminées en dérivant l'équation (2) et on obtient le résultat remarquable

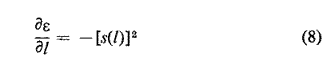
Il en résulte que n'est jamais positif, et la moyenne quadratique des modifications requises diminue toujours quand on répartit les modifications de perce sur une plus grande longueur de tube.

Résultats asymptotiques
Les valeurs propres de rang élevé d'une équation de Sturm-Liouville ont une distribution asymptotique simple9. Quand n est grand, fn ~ nc/2L et

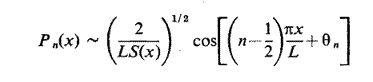
où qn dépend des conditions aux limites. Les instruments de musique tels que la trompette ont évolué vers une forme telle que les fréquences des résonances sont presque uniformément espacées. En d'autres termes, la formule fn ~ nc/2L, qui peut être prouvée pour n suffisamment grand, est en fait presque exacte pour tout n. Ceci suggère que les fonctions propres asymptotiques associées, Pn(x), pourraient être de bonnes approximations pour tout n. Ceci éviterait la mesure difficile de Pn(x). Si les conditions aux limites de la trompette sont approximativement

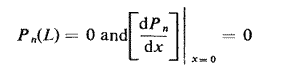
on peut montrer que

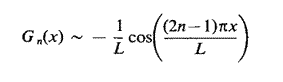
Les intégrales impliquées dans les calculs peuvent être maintenant évaluées analytiquement.
Nous avons testé ces calculs en imposant des valeurs à fn, en calculant la forme de perce requise à partir de l'expression asymptotique de Gn(x) puis en calculant les décalages de fréquence exacts (équation 2) que cette forme de perce produirait, en utilisant les vraies valeurs mesurées de Gn(x). Les variations de perce se sont avérées être dans le bon sens mais avec des erreurs importantes. Les résultats asymptotiques peuvent néanmoins être utilisées avec profit si (a) on a besoin d'une approximation rapide (la mesure des Pn(x) prend du temps), ou si (b) un partiel de rang très élevé nécessite une correction, là où il est impossible de mesurer la résonance.

Vérification de la théorie
La trompette a été excitée par l'appareil automatique décrit dans la première section et la pression acoustique a été mesurée de deux manières : en utilisant des tubes de sonde insérés radialement dans des trous pratiqués tous les centimètres sur la longueur de l'instrument, ou en utilisant une longue sonde flexible enfilée dans l'instrument. Il y a peu d'écart entre les résultats de l'une ou l'autre méthode qui sont présentés avec les fonctions calculées Gn(x) à la figure 3.

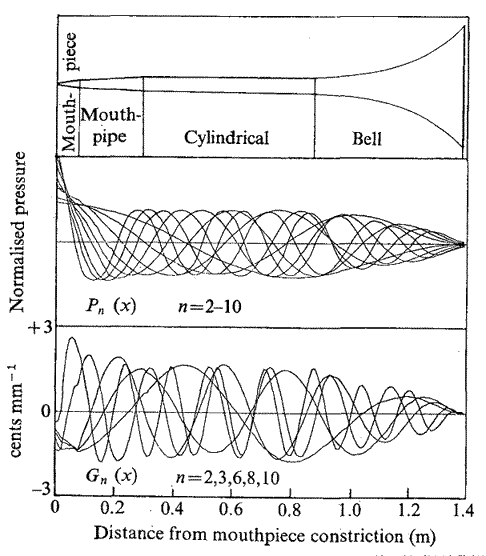
Fig. 3 Forme de perce réelle d'une trompette (schéma sans échelle) avec Pn(x) et Gn(x) pour quelques modes choisis.



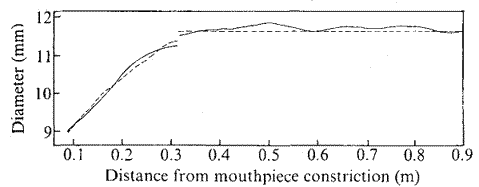
Fig. 4 La forme de perce d'une trompette (parties conique et cylindrique)
avant et après modification :____ perce modifiée ; ----- perce originale .
( NdT : distance mesurée à partir du grain de l'embouchure)

Dans un précédent paragraphe, on a évoqué la difficulté du choix de la justesse optimale d'un instrument. Pour vérifier nos idées, nous avons choisi d'imposer arbitrairement les modifications suivantes : pour les cinquième et dixième résonance, un changement de +5 cents, pour la sixième résonance un changement de -5 cents, et les autres résonances inchangées. De même, la longueur sur laquelle portent les modifications de perce a été arbitrairement limitée à 0,9 m à partir de l'embouchure de l'instrument.

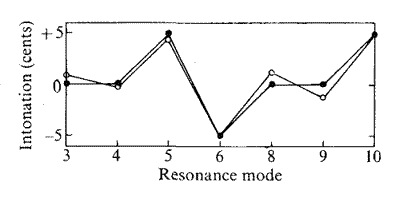
Fig. 5 Justesse relative de sept modes de résonance.
• : changement de hauteur exigé ; o : changement obtenu par la modification de perce.

Cette perce correspond aux notes "à vide" de l'instrument et des longueurs de tube additionnelles sont insérées par les pistons pour produire une gamme chromatique. En conséquence l'effet de notre modification est susceptible d'être moins précis quand on ajoute des longueurs de tube ; la méthode des perturbations pourrait être appliquée aux tubes additionnels des pistons pour corriger les notes qui les utilisent. L'équation (8) implique qu'en raison de la longueur relativement courte de la tuyauterie des pistons, seules de petites corrections de justesse pourraient être faites de cette façon sans nécessiter des variations de diamètre importantes et inacceptables.

Fig. 6 Spectre de la note Ré5 (587.33 Hz) jouée par un musicien professionnel
(a) avant et (b) après modification.
Les deux notes ont été jouées mezzoforte dans une chambre sourde
avec le microphone à 1 m dans l'axe de l'instrument .

Le graphique de la nouvelle forme de perce (fig. 4) montre un changement maximum de diamètre < 0,2 millimètre. Ceci peut être comparé à un maximum de 0,14 millimètre pour la plus petite perturbation en moyenne quadratique citée précédemment.
La nouvelle forme a été reproduite avec une résine renforcé par fibres de verre et ses résonances ont été mesurées à l'aide de l'appareil automatique. Il y a une correspondance étroite entre les justesses requise et mesurée (fig. 5) ; les petites erreurs résultent principalement de la difficulté à produire une nouvelle perce avec une précision meilleure que 0,02 millimètre.
On peut déduire de l'analyse qualitative des effets de changements de diamètre aux nœuds et aux ventres de vibration que certains décalages de fréquence imposés peuvent exiger des changements contradictoires de diamètre. Le résultat dans ces cas est que des augmentations et des diminutions très importantes de diamètre sont exigées sur des distances courtes. Elles seraient inacceptables sur un instrument de musique et rendraient également invalide notre théorie des perturbations au premier ordre. Notre procédé d'optimisation assure que des changements importants de diamètre ne sont pas appliqués inutilement.
Pour la comparaison on a effectué un autre calcul qui suppose une forme de perce non-optimum donnée par superposition d'ondes sinusoïdales. Le changement maximum de diamètre exigé ici était de 3 millimètres.

Corriger une trompette défectueuse
Bien que la théorie précédente ne convienne pas idéalement à la conception acoustique complète d'un nouvel instrument, la meilleure application de ce travail est l'amélioration des différentes notes d'instruments prototypes ou de production. Un tel instrument s'est avéré avoir une deuxième harmonique faible en jouant le Ré5 (587,33 Hertz) (Fig. 6a). Comme on l'a déjà mentionné, cette harmonique mobilise la dixième résonance pour se renforcer, qui s'est avérée basse par rapport à la cinquième. La dixième résonance n'est pas normalement jouée en tant que fondamental et par conséquent on peut la modifier pour améliorer le timbre. En utilisant notre nouvelle technique nous avons pu faire monter cette dixième résonance de dix cents pour améliorer la réponse (Fig. 6b).
Ce travail a été soutenu en partie par le SRC et Boosey & Hawkes Ltd. Nous remercions le Dr. D. M. A. Mercer pour ses encouragements et sommes reconnaissants également de l'aide de M. W. Tompkins et du trompettiste Michael Laird.

Reçu le 13 mai ; accepté le 21 juillet 1976 et publié dans Nature, vol. 262 du 26 août 1976, pp. 761-765.

1 Smith, R. A., thèse de doctorat, Univ. Southampton (1974) .
2 Martin, D. W., thèse, Univ. Illinois (1941).
3 Webster, J. C, J. acoust. Soc. Am., 19, 902-906 (1947).
4 Igarashi, J., et Koyasu, M., J. acoust. Soc. Am., 25, 122-128 (1953).
5 Hunt, F. V., J. acoust. Soc. Am., 10, 216-227 (1939).
6 Backus, J., et Hundley, T. C, J. acoust. Soc. Am., 49, 509-519 (1970).
7 Benade, A. H., et Jansson, E. V., Technical Report (Speech Transmission Laboratory, Royal Institute of Technology, Stockholm, 1973).
8 Morse, P. M., Vibration and Sound, 2nd ed., 269 (McGraw-Hill, New York, 1948).
9 Morse, P. M., et Feshbach, H., Methods of Theoretical Physics, par. 6.3 (McGraw-Hill, New York, 1953)

Traduit en janvier 2004 par Joël Eymard pour le site web "Tout sur la trompette"