35. Interaction entre colonne d'air, anche et voies respiratoires du musicien dans les instruments à vent.

Arthur H. Benade

Extrait de Vocal Fold Physiology: Biomechanics, Acoustics and Phonatory Control, Denver Center For Performing Arts (1985), ed Titze and Scherer.
Original version in English

RÉSUMÉ

Les instrumentistes ont toujours insisté sur l'importance d'obtenir une configuration correcte de leur voies respiratoires. C'est pourquoi les succès apparents de la théorie usuelle des anches vibrantes et des colonnes d'air musicales, qui ne tient pas compte des effets de la colonne d'air interne de l'instrumentiste, sont devenus de plus en plus mystérieux au fur et à mesure que le sujet mûrissait. Puisque cette théorie a été utile jusqu'à présent pour guider la construction de bons instruments, la confiance en ces techniques est suffisante pour permettre d'aborder sérieusement le problème de son extension incluant les voies respiratoires de l'instrumentiste. La plus grande part de l'énergie est produite à des fréquences où A[(Z_u + Z_d)//Z_r]≈>l. Ici, A et Z_r sont la transconductance et l'impédance de l'anche tandis que Z_u et Z_d sont les impédances d'entrée des colonnes d'air vues en amont et en aval de l'anche. Des effets non-linéaires couplent ces sources d'énergie via une action hétérodyne, que l'on prenne en compte Z_u ou non. Le développement des techniques de mesure par FFT et réflectométrie d'impulsion pour les impédances des colonnes d'air de l'instrument et du musicien ont permis une extension significative de la théorie. La plupart des configurations de voyelles (supraglottales) créent des pics d'impédance Z_u dans la gamme des 450 à 1500 Hz qui sont capables de jouer un rôle important pour les instruments. Le fait que ces pics ne coïncident pas avec les fréquences des formants de la parole a contribué à entretenir la confusion, de même que le fait que certains instrumentistes utilisent inconsciemment les résonances de leurs voies respiratoires alors que beaucoup ne les utilisent pas du tout.

I. INTRODUCTION

Ce rapport a pour but de fournir un compte-rendu préliminaire sur la façon dont les voies respiratoires de l'instrumentiste interagissent avec la colonne d'air et l'anche d'un instrument à vent. Nous avons aujourd'hui une très bonne compréhension théorique de l'interaction entre l'anche et la colonne d'air, dans la mesure où il est possible non seulement de décrire la nature acoustique de l'interaction mais également de l'utiliser comme un guide efficace du facteur d'instruments dans ses efforts pour construire un bon instrument ou pour en améliorer un déjà existant. C'est pourquoi notre mission est relativement simple : nous devons seulement montrer comment les complexités additionnelles liées à la colonne d'air de l'instrumentiste modifient la physique mathématique du système plus simple anche/colonne d'air, puis examiner la façon dont le système modifié diffère dans son comportement de celui qui a été complètement étudié.

La première réaction du lecteur au paragraphe précédent pourrait bien être une remarque du genre : "depuis des centaines d'années les musiciens ont insisté sur l'importance de la configuration de la bouche et de la gorge de toute personne qui veut jouer d'un instrument à vent à un bon niveau. Comment alors peut-on prétendre sérieusement avoir compris un instrument à vent sans tenir compte de ce fait ? En outre, comment peut-on ensuite présenter l'importance de la colonne d'air interne de l'instrumentiste comme une nouvelle découverte ?" J'espère que les réponses à ces questions importantes vont d'elles-mêmes clarifier la nature de ce qui a été nouvellement compris.

Pendant de nombreuses années j'ai vaillamment dit à mes amis musiciens (et à moi-même, dans mon incarnation en tant qu'instrumentiste amateur sérieux) que le rôle de la colonne d'air de l'instrumentiste pourrait être clarifié seulement après que les autres facteurs plus évidents de la vibration musicale auraient été correctement élucidés.

En fait, aujourd'hui la question s'est inversée, prenant la forme : "comment une partie aussi largement influente du système dynamique a pu rester incognito pendant des années d'investigations où des modifications de seulement deux ou trois paramètres acoustiques parmi des milliers d'autres pouvaient aisément être associés à leurs conséquences dynamiques et musicales?"

Il sera peut-être utile de reformuler les remarques précédentes de la façon suivante avant que nous regardions la physique elle-même.
LES VOIES RESPIRATOIRES DES POUMONS A LA BOUCHE INFLUENCENT-ELLES DE MANIÈRE SIGNIFICATIVE LE JEU DES INSTRUMENTS A VENT ?
1.      LES MUSICIENS SONT UNANIMES POUR DIRE QUE OUI.
2.     L'ACOUSTICIEN MUSICAL A EU TENDANCE À IGNORER LA QUESTION, OU À LA METTRE DE CÔTÉ COMME UNE INFLUENCE RELATIVEMENT PETITE.

Le point (2) ci-dessus est une simplification délibérément exagérée. Des mesures et des spéculations d'une nature acoustique ont été faites au cours des décennies, mais pour différentes raisons aucun consensus clair ne s'est développé. Le récit détaillé de cette branche de l'histoire ne contribuera pas de façon appréciable à notre but actuel, qui est de donner une description concise de ce qui est connu aujourd'hui, sous une forme qui (si tout va bien) soit intelligible à un lectorat qui s'intéresse principalement à la biophysique de l'instrumentiste lui-même plutôt qu'aux détails de son interaction avec un instrument à vent.

Arrivé à ce point de mes observations préliminaires, je voudrais qu'il soit clair que le présent rapport veut être un peu plus qu'une annonce de certains des résultats récents obtenus à Cleveland. Pour la brièveté, je courrai donc le risque de frustrer mes lecteurs et d'ennuyer d'autres chercheurs dont les résultats n'y sont pas correctement cités. Je mentionnerai cependant ici le nom ceux de mes collègues passés et présents qui ont apporté une contribution particulièrement large (au delà des limites de leurs publications) aux investigations rapportées ici ; ce sont Walter Worman, George Jameson, Stephen Thompson, et Peter Hoekje. Le présent rapport n'aurait pas été possible sans leur collaboration directe. C'est vrai de George Jameson et de Peter Hoekje en particulier. A part cela, je présenterai seulement les détails bibliographiques qui peuvent directement aider le lecteur dans sa compréhension de la discussion actuelle. Un rapport formel de recherches avec les références et la documentation appropriées est préparé par Hoekje et moi-même pour être soumis au Journal of the Acoustical Society of America.

II. FORMULATION DU PROBLÈME

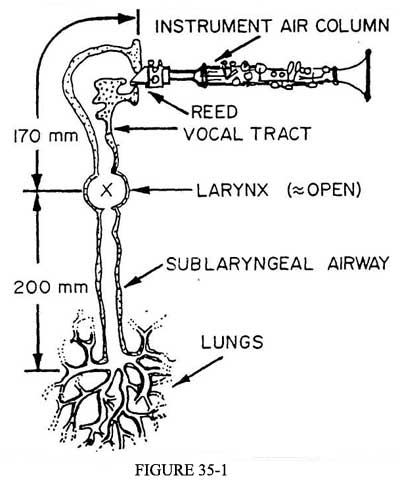
La figure 35-1 montre la nature générale du système dynamique considéré. Le système peut être considéré comme la concaténation de quatre segments principaux : le conduit sublaryngal (terminé à son extrémité inférieure par les poumons de l'instrumentiste), le larynx (qui dans le cas présent est soit grand ouvert soit partiellement fermé d'une façon qui ne lui permet pas de vibrer), le tractus vocal (qui est largement réglable par l'intermédiaire des mouvements du palais mou, de la langue, des mâchoires, etc..), l'anche de l'instrument de musique (dont le point de fonctionnement, l'amortissement, etc., sont commandé par la position et la pression des lèvres de l'instrumentiste), et la colonne d'air musicale (dont les propriétés acoustiques sont commandées par l'intermédiaire des doigts de l'instrumentiste sur les divers clefs et/ou trous).

Dans tout instrument à vent, bois, cuivre, voix (ou même harmonica !), nous trouvons trois sous-ensembles en interaction : un conduit d'air de l'émetteur de vent (la colonne d'air interne de l'instrumentiste ou le pied du tuyau d'orgue et la boîte à vent située en-dessous), un dispositif de régulation de débit (l'anche de roseau ou les lèvres pour un instrument à vent orchestral, le larynx du chanteur, l'anche libre de l'harmonica, ou l'anche d'air du flûtiste), et enfin une certaine sorte de résonateur et de système de rayonnement qui assure le couplage final à la salle dans laquelle le son doit être émis. Mettant de côté la famille des flûtes, le dispositif de commande d'écoulement est un piston dont le degré de fermeture est déterminé par la différence de pression entre les deux côtés d'une surface de fonctionnement.

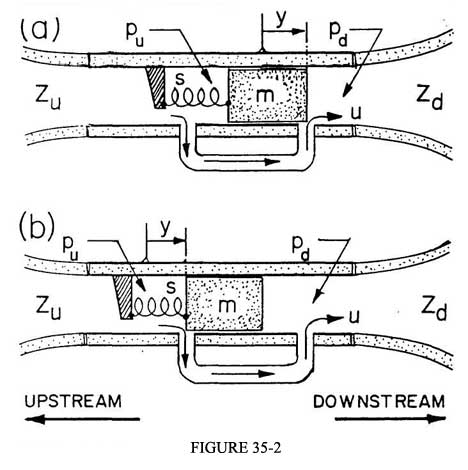
La figure 35-2 présente deux versions du système basique commandé par la pression. L'une des pressions de commande est maintenue en partie par les poumons et produite en partie par les perturbations acoustiques ayant leur origine dans le conduit respiratoire de l'instrumentiste (en abrégé PWW pour "player's wind-way"). L'autre pression agissant sur la valve (l'anche) provient de l'embouchure de l'instrument et résulte de l'activité acoustique qui se produit dans la colonne d'air de l'instrument (en abrégé IAC pour "instrument air column"). Dans la figure 35-2a le fonctionnement de la valve est tel qu'une augmentation de pression en aval p_d entraîne une augmentation de débit. Ce fonctionnement est typique des instruments à anche d'orchestre et des jeux d'orgue à anche. La figure 35-2b montre, au contraire, un système où le fonctionnement de la valve est inversé et où une augmentation de p_d réduit le débit u, fonctionnement typique des cuivres.

Par commodité, nous définirons les directions dans ce système de guide d'ondes pratiquement uni-dimensionnel à l'aide des termes "amont" et "aval", par référence au sens d'écoulement de l'air depuis les poumons de l'instrumentiste jusqu'à la pièce dans laquelle il joue. Ainsi l'une des pressions qui commandent le débit agit sur le côté amont de l'anche tandis que l'autre s'exerce sur le côté aval. La terminologie basée sur cette convention empêche les ambigüités du genre de celles que produirait l'utilisation des mots "haut" et "bas". Pour un clarinettiste, l'air circule vers le haut dans les voies respiratoires puis vers le bas dans l'instrument. Imaginez de décrire de la même façon ce qui se passe dans un tuba ou un basson !

Il est commode aussi de caractériser le PWW et la IAC par leurs impédances vues par le contrôleur de débit. On désignera par Z_u l'impédance du PWW vue en amont, tandis que l'impédance de la IAC sera notée Z_d. L'anche elle-même nécessite deux caractérisations, puisqu'elle joue deux rôles dans le système vibratoire complet. Nous définirons son impédance acoustique Z_r comme la vitesse du volume qu'elle déplace quand elle bouge en réponse à une variation de pression exercée sur l'une quelconque de ses faces (voir la figure 35-2) ; l'autre propriété, peut-être la plus basique, est sa caractéristique de contrôle de débit qui est en général une fonction non linéaire. Cette caractéristique de contrôle de flux est le plus commodément spécifiée en exprimant le débit u par un développement de Taylor en fonction de la différence de pression p entre les deux faces de l'anche, comme dans l'équation 35-1.

u(t) = u₀ + A p(t) + B p²(t) + C p³(t) + + + + +                    (35-1)

Comme l'anche fonctionne comme un système ressort-masse-amortisseur, on voit d'emblée que Z_r présente une propriété de résonance qui la rend inversement proportionnelle au facteur D(ω) défini dans l'équation 35-2.

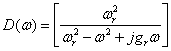                                                   (35-2)

Ici ω_r est la fréquence naturelle de l'anche et g_r est sa bande passante à demi-puissance. On voit en outre que puisque le débit d'air qui franchit l'anche dépend de sa position (et donc indirectement de la pression qui agit sur elle), les coefficients de contrôle de débit sont eux-mêmes résonants par nature. C'est à dire que ces coefficients peuvent s'exprimer comme le produit de leur valeur à un régime permanent de basse fréquence (A₀, B₀, C₀, . . .) par le facteur D(ω) défini ci-dessus. Ce fait se révèle très important pour notre compréhension du jeu des instruments. On peut utilement remarquer que A₀ est positif pour le système de valve des "bois" de la figure 35-2a et négatif pour celui des "cuivres", représenté sur la figure 35-2b.

Exprimons maintenant la relation entre pression et débit sur les faces amont et aval de l'anche, en termes d'impédances Z_u, Z_d, and Z_r. La direction positive du flux acoustique est définie comme le sens d'écoulement du flux d'air continu provenant des poumons du musicien.

u = p_d/Z_d + (p_d - p_u)/Z_r                                                                     (35-3a)

-u = p_u/Z_u + (p_u - p_d)/Z_r                                                                    (35-3b)

Le premier terme du membre de droite de chacune de ces équations exprime simplement la relation ordinaire entre la pression à l'entrée d'un guide d'onde et le débit qui y pénètre. Le second terme donne la mesure du flux qui occupe le volume balayé par l'anche elle-même quand elle se déplace sous l'influence de la différence de pression entre ses deux faces.

Les équations 35-3a et 35-3b peuvent être combinées d'une façon intéressante et utile : le débit u qui passe par l'ouverture de l'anche s'exprime très simplement en fonction de la différence de pression p entre les faces de l'anche comme le montre l'équation 35-4.

p = u(Z_u + Z_d)//Z_r                                                                               (35-4)

Autrement dit, la différence de pression de part et d'autre de l'anche est proportionnelle à la somme des impédances amont et aval, en parallèle avec l'impédance de l'anche (qui tend à être très grande comparée aux autres impédances, de sorte qu'elle a un rôle secondaire, quoique non-trivial, dans le processus d'oscillation). Cette impédance combinée sera notée Z sans indice.

Pour préparer la prochaine étape de la discussion, il faut récapituler la nature du problème dont nous essayons de décrire la solution. Quand on joue d'un instrument à vent, les impédances amont et aval (ainsi que l'impédance propre de l'anche) sont couplées aux poumons, source principale de la pression d'air, via une valve contrôlant le débit. Le système est maintenu en oscillation par une boucle de rétroaction dans laquelle la perturbation acoustique au niveau de l'anche (c'est à dire la différence de pression entre ses faces) commande le contrôleur de débit, et le débit résultant sert d'excitateur pour les ondes amont et aval.

L'équation 35-1 nous donne une représentation formelle de la propriété de l'anche comme contrôleur de débit commandé par la pression u(p), tandis que l'équation 35-4 représente de façon très compacte la réponse en pression du système global (PWW + IAC + anche) à une variation de débit. Notons que les deux équations relient le débit u, qui est le même des deux côtés de l'anche, à la différence de pression p entre ses faces. En d'autres termes, notre analyse peut se focaliser sur p et u via l'impédance combinée Z et le "polynôme de contrôle" u(p), sans avoir à se préoccuper des complications des réponses individuelles de nos trois sous-systèmes au flux qu'ils engendrent conjointement via un couplage non linéaire.

Du point de vue de la physique mathématique nous avons ici une première explication de la raison pour laquelle les effets produits par le PWW n'ont pas automatiquement détruit notre capacité à effectuer des calculs significatifs guidés, et vérifiés, par des expériences avec des anches et divers types d'IAC - il suffisait que le PWW ne produise pas d'effet antagoniste ou masquant. Nous avons eu la chance, en effet, pendant de nombreuses années que ce soit le cas assez longtemps pour nous permettre d'appréhender solidement la physique essentielle.

Revenons maintenant rapidement à la façon dont le comportement essentiel du système peut être compris. En nous limitant pour le moment au cas d'oscillations strictement périodiques dans le système, nous exprimons le débit u(t) par une série de Fourier :
u(t) = Σu_ncos(nω₀t + ψ_n)                                                                      (35-5)

Ici ω₀ représente la fréquence du son produit. Terme par terme, cette série représente le spectre du flux d'excitation appliqué au système (PWW + IAC + anche). Étant donnée l'impédance (nette) Z(ω) de ce système, on note Z_n son amplitude à la fréquence nω₀ et Φ_n sa phase. La pression correspondant à u(t) peut s'exprimer par :

p(t) = ΣZ_nu_ncos(nω₀t + ψ_n + Φ_n)                                                          (35-6)

S'agissant de mathématiques formelles, les équations 35-1, 35-5, et 35-6 peuvent être résolues simultanément pour donner le spectre de pression à travers l'anche pour une pression de souffle donnée. Tandis que les calculs détaillés sont très pénibles, il apparaît possible d'extraire beaucoup d'informations utiles sur le système. Cette information, qui peut être aisément vérifiée sur le comportement de systèmes réels, dépend bien davantage de la structure mathématique globale du problème que des valeurs numériques des divers paramètres. C'est-à-dire que les caractéristiques marquantes de la solution peuvent être récapitulées très simplement sous une forme qui dépend seulement du comportement systématique des équations trigonométriques non-linéaires. En outre, quand on résout l'ensemble, on trouve (assez étonnamment) que les résultats ne montrent presque aucune sensibilité aux phases des impédances ni au facteur de résonance de l'anche (équation 35-2) ! Cela ne veut pas dire que les phases sont non pertinentes ou qu'elles ont des valeurs aléatoires - simplement que les amplitudes de spectre ne sont pas sensibles aux phases des Z_n et des D_n.

Les équations 35-7 et 35-8 suffiront ici pour indiquer la nature du spectre de pression de jeu mesuré à travers l'anche. En particulier, le composant fondamental p_l, qui est l'amplitude de pression de la perturbation à la fréquence jouée, obéit à une équation de la forme :

                                                                  (35-7)

De même, les composantes plus élevés ont des amplitudes qui peuvent tout être écrites sous la forme :

                                                                   (35-8)

Je précise que dans ces équations il n'y a aucune manifestation explicite des déphasages liés aux paramètres de régulation de débit ou aux impédances. Seules les amplitudes sont importantes quand l'oscillation est de type périodique.

Nous remettrons à plus tard la discussion de ces résultats jusqu'à ce que nous ayons esquissé la description d'un cousin linéaire de cette analyse, dans lequel nous pouvons voir ce qui arrive au n^ième composant de la pression considéré pour lui-même, le couplage non-linéaire indéniable entre les composants spectraux étant représenté par une source de flux U_n qui est "externe" au composant en question.

III. UN COUSIN LINÉAIRE DU PROBLÈME

Supposons que notre système oscille en régime stationnaire à la fréquence ω₀, avec une partie u(t) du flux produite par le terme linéaire Ap du polynôme de contrôle, et une partie U(t) imposée de l'extérieur par une source, jusqu'ici non spécifiée, de même périodicité. Si nous utilisons la représentation de Fourier, le flux imposé peut s'écrire :

U(t) = ΣU_ne^jnω0t                                                                                     (35.9)

et le signal de pression à travers l'anche est :

p(t) = ΣZ_n[u_n + U_n]e^jnω0t                                                                       (35.10)

L'équation 35-10 peut être résolue terme par terme pour les amplitudes des composantes du flux en termes d'impédances combinées Z_n et de transconductances correspondantes A_n (évaluées aux fréquences ω_n considérées) :

u_n = A_np_n = Z_nA_n[u_n + U_n]                                                                      (35-11)

d'où :

u_n = U_n[(Z_nA_n)/(1 - Z_nA_n)]                                                                      (35-12)

Ici et dans la discussion qui suit avec l'équation 35-13, les symboles A_n et Z_n ont leur représentation complexe habituelle, c'est à dire que l'on prend en compte à la fois l'amplitude et la phase. L'équation 35-12 a la forme familière qui représente le gain en courant u_n/U_n d'un amplificateur à rétroaction dont le gain en boucle ouverte est Z_nA_n. On voit immédiatement, par conséquent, que chaque composant spectral du flux se comporte comme un oscillateur indépendant auto-entretenu si la partie réelle du gain en boucle ouverte est exactement l'unité. C'est à dire qu'il n'est pas nécessaire de recevoir un apport d'énergie externe par le signal excitateur U_n pour maintenir l'oscillation.

En revanche, si le gain en boucle ouverte Z_nA_n est inférieur à 1, l'amplitude du composant de flux u_n est proportionnelle à U_n. De plus, l'amplitude de u_n va décroître exponentiellement jusqu'à zéro si U_n est subitement arrêté, avec un taux de décroissance proportionnel à la différence entre 1 et la partie réelle de Z_nA_n.

Si, d'autre part, le gain en boucle ouverte est supérieur à 1, une oscillation exponentiellement croissante peut se produire avec un taux de croissance qui est de nouveau proportionnel à la différence entre 1 et la partie réelle du gain en boucle ouverte. Dans ces conditions le système de rétroaction peut (pour le composant en question) produire plus d'énergie qu'il ne peut en dissiper, sans nécessiter d'apport additionnel via U_n.

Pour autant que notre présent modèle (trop simplifié) est concerné, nous pouvons résumer en disant que l'oscillation de chaque composant spectral est indépendante des autres, et qu'elle est par nature instable. Nous sommes évidemment bien habitués à cette sorte d'instabilité, qui est partagée par tous les oscillateurs ordinaires, et il est tout à fait usuel de rappeler la présence d'un amortissement additionnel (non-linéaire) dépendant de l'amplitude qui entre en jeu pour stabiliser l'amplitude d'un oscillateur réel.

Dans l'oscillateur musical à plusieurs composants il y a, bien sûr, plusieurs sources d'amortissement en fonction de l'amplitude, en plus de celles qu'impliquent Z_u, Z_d et Z_r (l'amortissement par turbulence, par exemple). Il y a, cependant, une autre manière dont de l'énergie peut être transférée dans et hors de chaque composant spectral, une manière qui assure non seulement la stabilité de chaque amplitude composante sous des conditions beaucoup moins rigoureuses sur le gain en boucle ouverte, mais garantit également que les diverses amplitudes ont un rapport bien défini entre elles. C'est naturellement une condition absolue pour une source de son musical dont le timbre doit être défini pour chaque façon de jouer choisie par son utilisateur. La nature fondamentalement non-linéaire du polynôme de commande défini dans l'équation 35-1 montre (en termes les plus simples) que quels que soient les composants p_n du signal de pression pouvant être produits par l'intermédiaire du terme linéaire de ce polynôme, ils contribueront immédiatement à l'ensemble de composants du flux à toutes autres fréquences harmoniques selon l'arithmétique hétérodyne (intermodulation) qui peut être généralisée pour des exposants arbitraires selon la relation trigonométrique :

(McosP) (NcosQ) = (MN/2)[cos(P+Q) + cos(P-Q)]                            (35-13)

C'est-à-dire qu'on peut maintenant comprendre que les composants "imposés extérieurement" U_n de flux qui ont été présentés dans l'équation 35-9 représentent d'une manière très simple (informatiquement inutile mais utile heuristiquement) le transfert d'énergie de chaque oscillateur modal vers ses frères. Il n'est plus nécessaire que chaque composant soit précisément auto-entretenu quand on le considère isolément ; tout ce qui est exigé est que en tant que groupe les composants spectraux puissent conjointement produire assez d'énergie pour fournir leur apport énergétique total au monde extérieur.

Notre modèle quasi-linéaire nous montre encore un autre aspect de la nature du système non-linéaire réel : chaque composant spectral est relié directement ou indirectement à tous les autres, de sorte que sa phase est la résultante de nombreuses influences. La nature de l'oscillation est telle qu'il y a beaucoup de façons dont la phase réelle d'un composant donné peut être réconciliée avec celles de ses confrères. Une analyse appropriée prouve que, en conséquence, les amplitudes spectrales sont déterminées presque exclusivement par les valeurs des paramètres Z et A, B, C appropriés et pas par leurs angles de phase (Thompson 1978).

La discussion jusqu'ici dans ce paragraphe a montré que la production énergétique est favorisée aux maxima du produit A(ω)Z(ω). Dans les instruments de la famille des bois, A est très proche de A₀ sur la plus grande partie du spectre car la fréquence de résonance propre de l'anche ω_r est relativement élevée (de l'ordre de 2000 à 3000 Hz pour une clarinette). Dans ces conditions, la production d'énergie est favorisée aux maxima d'impédance du système PWW-IAC-anche. Ceci indique (si on ignore provisoirement Z_u et Z_r) que l'oscillation est favorisée aux fréquences des modes normaux de la IAC prise avec son extrémité côté anche fermée, comme cela a été reconnu depuis au moins 200 ans ("la clarinette joue comme un tuyau fermé").

Une autre implication de notre discussion est que la production énergétique globale est la plus grande si les maxima d'impédance sont en relation harmonique entre eux. Ceci assure que chacun des composants de fréquence hétérodyne produits par les harmoniques de la note jouée se trouve lui-même à un des maxima d'impédance qui produisent l'énergie et transfère de ce fait l'énergie à un endroit productif dans le processus de régénération. Exprimons ceci dans des termes plus proches de la musique comme on le faisait avant d'inclure explicitement les effets du PWW : un instrument de musique dont les maxima d'impédance (modifiés par l'impédance Z_r parallèle mais grande) sont en relation harmonique est un instrument qui a une bonne attaque des sons, produit un son propre, fournit une dynamique contrôlable et des hauteurs de sons stables, et est en tous points des plus agréables entre les mains de l'instrumentiste et pour les oreilles de l'auditeur. J'ai présenté une discussion très étendue de ces questions dans les chapitres 20 à 22 de mon livre (Benade 1976). La reconnaissance de l'utilité d'un "alignement" harmonique précis des résonances de la colonne d'air a mené (depuis les environs de 1964) à une évolution continue des techniques de laboratoire et de fabrication pour la mesure et la correction des positions des résonances appartenant à pratiquement toutes les notes de la tessiture d'un instrument. Le comportement des instruments ajustés au moyen de ces techniques a été beaucoup admiré par des musiciens renommés, et les techniques elles-mêmes commencent à avoir un effet significatif sur la fabrication de tous les types d'instruments aujourd'hui (du moins ceux de qualité professionnelle)

Nous avions temporairement mis de côté la possibilité que le produit ZA puisse devenir grand au voisinage de la fréquence de l'anche ω_r, de sorte que l'harmonique pour laquelle nω₀≈ω_r pourrait contribuer à la production nette d'énergie même si l'impédance Z elle-même n'est pas grande. Tandis que le livre contient de nombreuses remarques qualitatives au sujet de l'utilité musicale de cette possibilité pour les bois, la physique détaillée n'en a été élucidée que plus tard (Thompson 1979). Pour la présente étude il suffira de dire que tous les joueurs d'instruments à anches de haut niveau exploitent la possibilité d'une source d'énergie supplémentaire à la fréquence w_r en plaçant cette fréquence d'anche à une certaine harmonique (n'importe laquelle !) de la fréquence jouée afin de stabiliser et épurer encore plus leur son en incluant un participant supplémentaire exactement aligné dans le "régime d'oscillation." Pour les cuivres, l'instrumentiste doit faire attention à w_r, puisque la note qu'il souhaite jouer est choisie directement en ajustant la fréquence naturelle de l'anche-lèvre pour la mettre juste en dessous du fondamental du son désiré. Davantage de discussion de la dynamique curieuse des cuivres, avec leur valeur négative pour la transconductance d'anche A(w), nous emmènerait trop loin des buts de ce rapport. Il nous suffira de noter que la possibilité d'ajuster la fréquence de résonance de l'anche est une ressource musicalement importante pour le joueur d'instrument à anche et une nécessité inévitable pour le joueur de cuivres. Dans les deux cas nous constatons qu'un ajustement physiologique est employé comme une adjonction aux contrôles mécaniques exercés par les mains de l'instrumentiste sur les clefs, les pistons et les coulisses de son instrument.

Nous terminerons cette partie de notre petite présentation du mécanisme de production du son (par nature non-linéaire et donc très stable) des instruments à vent orchestraux en précisant une fois de plus que notre compréhension de ce mécanisme a atteint un niveau très élaboré sans tenir aucun compte de la possibilité que la colonne d'air de l'instrumentiste puisse elle-même jouer un rôle significatif. Notre analyse actuelle a prouvé que Z_u intervient dans les équations dynamiques d'une façon qui est entièrement symétrique de celle de Z_d. Pour le scientifique, ceci signifie qu'il n'a pas besoin de retoucher toutes ses équations quand il ajoute la prise en compte de Z_u à son analyse de Z_d et Z_r : le symbole Z prend simplement une signification légèrement différente. Du point de vue du musicien cela signifie que l'instrumentiste a une ressource d'ajustement physiologique additionnelle à sa disposition (dont nous pouvons maintenant voir la nature dynamique d'une manière générale). Pour nous tous, il reste pourtant la question de savoir pourquoi l'effet dynamique de cette ressource a pu demeurer scientifiquement ignorée pendant aussi longtemps, question à laquelle une réponse partielle sera donnée ci-dessous..

IV. IMPLICATIONS SPECTRALES

Maintenant que nous avons esquissé la nature générale du processus de régénération non-linéaire à plusieurs composants qui fonctionne dans les instruments à vent orchestraux, nous sommes en mesure d'examiner le spectre du signal de pression de commande p(t), donné dans les équations 35-7 et 35-8 ci-dessus. Rappelons que dans ces équations nous avons besoin seulement des amplitudes des paramètres Z, A, B, et C ! La première chose que nous notons est que les dénominateurs de ces équations sont presque exactement semblables au dénominateur de l'équation 35-12, de laquelle nous avons appris l'importance cruciale du produit Z_nA_n pour commander la quantité d'énergie qui peut être produite à la n^ième harmonique. Le seul aspect peu familier est la présence d'autres composants spectraux dont l'influence s'ajoute à l'effet direct du composant en question. Dans les équations 35-7 et 35-8 ces p_j supplémentaires sont les représentations explicites (dans une formulation pratiquement exacte) des contributions du "flux imposé" qui ont été présentées heuristiquement dans l'équation 35-9. Hormis ceci, les dénominateurs ont presque exactement la même signification dans la formulation exacte que dans notre version d'introduction. Nous pouvons le voir explicitement dans l'équation 35-7, qui fournit des informations sur le composant fondamental du spectre. Nous commençons en considérant la forme prise par cette équation dans la limite de basse amplitude, où les termes quadratiques et d'ordre supérieur dans le polynôme de flux (équation 35-1) n'ont aucun rôle à jouer. Dans ces conditions, le fait que p₂ et d'autres composants d'ordre supérieur soient nuls signifie que s'il y doit y avoir une quelconque oscillation à la fréquence fondamentale, alors (1 - Z_lA) doit disparaître, exactement comme nous en sommes arrivés à le prévoir.

Nous allons maintenant considérer le numérateur de l'équation 35-8. Il fournit un couple de conclusions globales remarquablement simples (qui sont bien justifiés par l'expérience dans des conditions appropriées), comme nous pouvons le voir dans la version simplifiée notée équation 35-14.

p_n = Z_np_lⁿ . (autres termes à variation lente)                                                   (35-14)

La première de ces conclusions est que la forme générale du spectre de pression contrôlée par l'anche est bien représentée par l'enveloppe de l'impédance globale de contrôle, et la seconde est que l'amplitude du n^ième composant de pression est proportionnel à la n^ième puissance de l'amplitude du fondamental quand celle-ci varie avec la pression de souffle de l'instrumentiste. En d'autres termes, quand on joue un crescendo en gardant son masque et son PWW inchangés, l'oscillation "se développe" depuis une sinusoïde presque pure vers une forme d'onde dont les composants grandissent progressivement jusqu'à la distribution pleinement développée du mezzoforte qu'implique l'équation 35-8. Mais en jouant plus fort, l'anche se ferme complètement pendant une fraction croissante de chaque cycle, provoquant un type entièrement nouveau de développement spectral qui a son enveloppe déterminée par la durée de passage des bouffées d'air par l'anche. Par ailleurs il faut seulement noter le parallélisme exact de forme mathématique entre les dénominateurs des équations 35-7 et 35-8.

Il est maintenant facile de décrire les deux spectres (qui peuvent être mesurés) de chaque côté de l'anche : c'est-à-dire le spectre mesuré dans l'embouchure de l'instrument (comme cela a été fait pendant de nombreuses années pour développer la théorie de base décrite ici) et le spectre mesuré dans la bouche de l'instrumentiste. Si nous notons (p_n)_u et (p_n)_d ces deux composants du spectre de pression et rappelons que

Z_n = ((Z_u + Z_d)//Z_r)_n ,

alors

(p_n)_u = u_n(Z_u)_n = p_n(Z_u /Z)_n                                                                  (35-15a)

(p_n)_d = u_n(Z_d)_n = p_n(Z_d /Z)_n                                                                  (35-15b)  

Si (comme on le sait depuis de nombreuses années), Z_r est assez grand pour n'avoir qu'une faible influence sur l'amplitude de Z, et si (comme on l'a supposé pendant presque aussi longtemps) Z_u est relativement petite et sans particularité, des équations comme 35-7 and 35-8 semblent s'appliquer directement au spectre dans l'embouchure, calculé en utilisant Z_d qui est obtenu par des mesures sur la IAC. En fait des expériences de cette sorte ont été réalisées et ont fourni une fraction significative de la preuve qui jusqu'à aujourd'hui a justifié notre confiance en la théorie ainsi décrite. Notons de nouveau ce que nous devons au fait étonnant mais bénéfique que nous n'ayons pas eu conscience de l'influence du PWW jusqu'à ce que nous ayons été prêts à le prendre en compte !

Il est évident que des variations des amplitudes du spectre de pression dans l'embouchure devraient directement refléter des changements des pics d'impédance correspondants, comme on le voit par le numérateur de l'équation 35-8 et le principal facteur dans l'équation 35-14. Il n'y a qu'un petit pas à franchir pour que nous invoquions la symétrie amont/aval du système comme justification de l'idée que des variations de Z_u produites par des mouvements de langue et de bouche de l'instrumentiste produiront exactement des changements parallèles du spectre de pression mesuré dans sa bouche. Mais on ne voit pas immédiatement ce qui arrive au spectre d'un côté de l'anche quand l'impédance varie de l'autre côté.

La différentiation de l'équation 35-15a par rapport à Z_u et de l'équation 35-15b par rapport à Z_d nous donne une représentation explicite des ces influences croisées. On obtient ainsi un résultat très étonnant :

EN PREMIÈRE APPROXIMATION, CHANGER Z D'UN CÔTÉ DE L'ANCHE NE PRODUIT AUCUN CHANGEMENT DU SPECTRE DE L'AUTRE CÔTÉ !

En y regardant de plus près nous constatons qu'il y a en effet de petits changements, particulièrement si le composant spectral perturbé est l'un de ceux pour lesquels le produit ZA est voisin de l'unité - si, en d'autres termes, il peut presque complètement équilibrer son propre budget d'énergie, et ainsi s'auto-entretenir sans fournir ni consommer l'énergie des autres composants.

Nous terminerons cette discussion de la formulation théorique globale du processus d'entretien des oscillations dans les instruments à vent par un court résumé des points principaux, laissant de côté des implications plus larges jusqu'après la présentation de quelques données expérimentales sur l'influence du PWW sur les régimes de jeu d'instruments réels. La première remarque qui doit être faite est que les impédances amont et aval apparaissent symétriquement dans la théorie. Le deuxième point est que tout ce qui concerne l'oscillation est directement déterminé par l'impédance combinée Z définie dans l'équation 35-4. Le troisième point est que si les maxima de Z sont en relation harmonique, l'oscillation est stabilisée, propre et contrôlable, ce qui favorise une bonne exécution musicale. En quatrième point, alors que des variations de Z_u et Z_d changent le spectre observable du côté où elles se produisent, il y a généralement peu ou pas de changement de l'autre côté de l'anche.

Le point trois ci-dessus peut nous donner une explication analytique de la raison pour laquelle un instrumentiste peut trouver avantageux de moduler son PWW. De même, le point quatre nous donne un indice sur la raison pour laquelle ces effets n'ont pas été immédiatement discernables au cours des recherche ou mesures habituelles faites seulement en aval de l'anche !

V. MESURE DE L'IMPÉDANCE DU CONDUIT RESPIRATOIRE DE L'INSTRUMENTISTE

Comme on l'a déjà remarqué, une des raisons pour pour lesquelles bon nombre d'entre nous ont tenu pour acquis que le PWW avait peu d'effet sur le processus de base d'entretien de la vibration dans un instrument à vent était l'hypothèse que les conduits ramifiés et à parois molles des poumons du musicien fonctionnaient comme une terminaison pratiquement non-réfléchissante du conduit sub- et supraglottal. Nous avons été encore encouragés dans la croyance que la colonne d'air en amont était peu susceptible d'avoir un rôle important par le fait que la base des tuyaux et la boîte à vent d'un orgue à tuyaux ont une influence relativement faible (mais pas musicalement négligeable !) sur le son et la stabilité des notes émises. Il y a vingt-cinq ans, ceci nous a donné une raison suffisante pour avancer hardiment, sur les conseils des écrits de Henri Bouasse (Bouasse, 1929-30), encouragés peu après par les premières mesures précises de la transconductance de régulation de débit de l'anche de clarinette (A_o) effectuée par John Backus (Backus 1963).

Alors qu'on pouvait faire des mesures précises des impédances d'entrée de la IAC dès le début de cette période active (voir des exemples de technique de mesure dans Benade 1973), les techniques de balayage des fréquences alors disponibles, nécessairement lentes, ne pourraient être adaptées aux mesures sur le PWW qui est hautement variable. L'arrivée plus récente de procédures commodes par FFT a amené bon nombre d'entre nous à concevoir des méthodes d'excitation par impulsion de flux, où l'impédance est déduite de la transformée de Fourier du signal de réponse de pression. Le lectorat de cet article étant bien plus au courant que moi de l'historique de ce sujet, la présente liste de références a seulement pour but d'en citer quelques uns qui ont influencé très tôt mes idées sur ce type de méthode (Oliver 1964 ; Rosenberg et Gordon 1966 ; Fransson 1975 ; Dawson 1976 ; Kruger 1980). Les autres paragraphes de ce chapitre seront consacrés d'abord à une indication de la nature de l'appareil que nous avons commencé à utiliser, puis à la présentation de l'impédance d'entrée du PWW (Z_u) mesurée pour différentes configurations de tractus, et finalement à une description d'une partie de l'information que l'on peut en tirer.

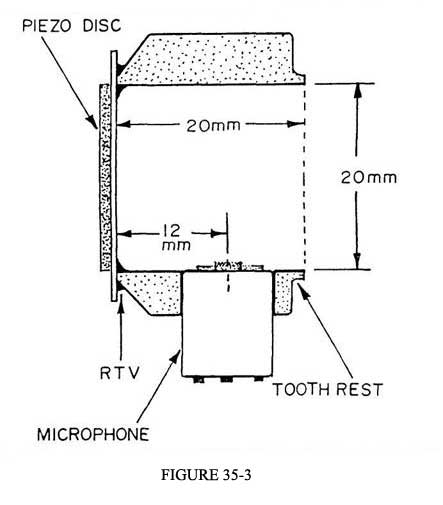
La tête de mesure d'impédance utilisée dans nos présentes expériences est du type représenté sur la figure 35-3 (Ibisi et Benade 1982). La source primaire de son est un disque piézoélectrique de "beeper" de 27 mm de diamètre collé sur l'extrémité d'un court morceau de tube en plastique à parois épaisses de 20 mm de diamètre intérieur et 32 mm de diamètre extérieur, par un joint en mastic de silicone. Le signal de pression est détecté par un microphone à électret dont l'ouverture de 3 mm débouche dans le tube à seulement 12 millimètres de la face interne du transducteur piézoélectrique. Si le transducteur piézoélectrique est considéré comme un oscillateur harmonique unimodal sans perte, alors un signal de tension en dent de scie à montée linéaire produira une impulsion simple de vélocité de la forme

v(t) = V[1 - cos(2πt/T)]                                                                       (35-16)

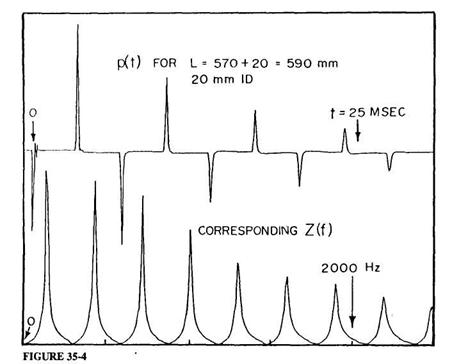
pour 0 < t < T (zéro ailleurs), pourvu que la durée T de montée en tension soit exactement égale à la période naturelle de vibration du transducteur. Seule une légère modification de la forme d'onde de la tension d'excitation est nécessaire pour assurer un signal d'excitation en vélocité très similaire quand on tient compte du fait que le transducteur est un oscillateur amorti (un rapport détaillé sur ce sujet, entre autres, est en préparation pour soumission au JASA*). Il suffit de dire que notre impulsion d'excitation a un FWHM d'environ 0.083 milliseconde, de sorte que la mesure par FFT de Z_u soit possible sans correction jusqu'à bien au delà de la limite de 2500 Hz de notre principal domaine d'étude.

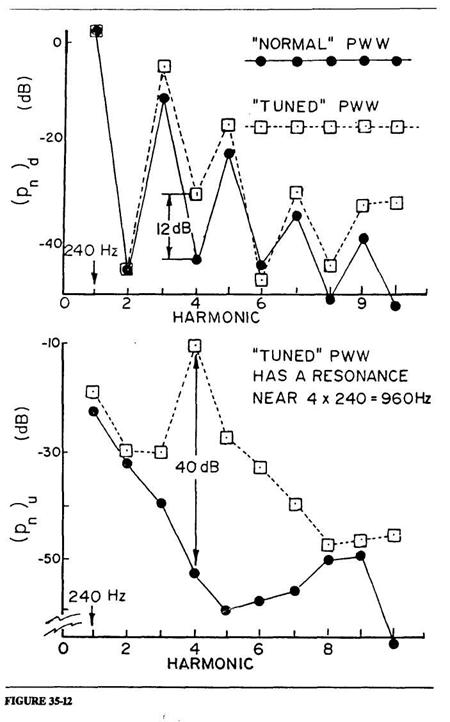La partie supérieure de la figure 35-4 montre la séquence d'impulsion-écho observée quand l'excitateur est fixé à un morceau de tube de cuivre de 20 mm de diamètre intérieur, ouvert à l'autre extrémité, et de 570 mm de long. Notons qu'en doublant l'amplitude de l'impulsion initiale, elle fait partie de la séquence des impulsions ultérieures alternées et décroissant exponentiellement, exactement comme la théorie le prévoit. La partie inférieure de la même figure montre l'impédance d'entrée de cette colonne d'air calculée par FFT à partir de l'onde fonction du temps de la partie supérieure de la figure. Ces deux courbes ont été tracées à partir des données stockées dans un analyseur en temps réel Hewlett-Packard 3582A.

La figure 35-5 donne une idée générale des valeurs maximales de Z_u et Z_d dans un contexte plus ou moins musical. Les échelles sont linéaires en Z et en fréquence. Le grand pic visible au voisinage de 1300 hertz appartient à Z_u mesurée dans les conditions suivantes : le sujet a formé son tractus de la façon usuelle pour articuler la voyelle [oh] et l'extrémité de la tête d'impédance a été insérée entre ses lèvres, ses dents reposant de part et d'autre de la tête d'impédance pour simuler l'espacement qu'elles ont sur un bec de clarinette. La séquence de pics de résonance moins élevés qui traversent tout le graphique reproduit la courbe d'impédance du tube de 20 mm de diamètre intérieur représenté sur la figure précédente. Les petits cercles placés au-dessus des pics de cette courbe d'impédance montrent où ils seraient placés si le diamètre du tube avait été de 15 mm au lieu de 20 mm. Ce diamètre de référence de 15 mm est choisi parce qu'il est très proche de la perce d'une clarinette en si bémol normale (dont les pics de résonance tendent en fait à être à peu près moitié moins hauts en raison de l'amortissement additionnel dû aux complexités des trous ouverts et fermés). Il est clair que les pics d'impédance du PWW peuvent être très sensiblement plus hauts que tous ceux que nous pourrions trouver dans une IAC réelle. Nous remettrons à plus tard toutes les implications de cette remarque jusqu'au paragraphe VI, après que nous ayons regardé un peu plus de données.

Les figures 35-6, 35-7 et 35-8 montrent les courbes de Z_u mesurée (en échelle logarithmique via la notation en dB) en fonction de la fréquence (en échelle linéaire) pour les voyelles [ah], [eh] et [ih]. Dans tous les cas les fréquences des principaux pics de résonance sont repérées, avec une indication de l'impédance d'onde d'un tube de 20 mm de diamètre interne que nous pouvons utiliser comme valeur de calibrage. Ce n'est pas par pure coïncidence que dans chacun des trois cas, aux limites de fréquence basse et haute des courbes, l'impédance mesurée correspond à cette valeur de référence. Nous reviendrons à une discussion de ce phénomène dès que les figures auront été décrites.

On voit une courbe en pointillés dans chacun des trois diagrammes d'impédance. Une courbe séparée de ce type a été à l'origine dessinée à main levée sur une copie de chaque courbe de résonance sur la base de critères qui deviendront clairs sous peu. On a alors vérifié que ces trois courbes étaient toutes très semblables. Une courbe moyenne unique a été alors construite par un procédé de lissage non formalisé. C'est cette courbe moyenne qui est représentée.

Dans la théorie des tuyaux sonores non-uniformes il est commode de définir l'impédance d'onde vue à l'entrée comme la fonction Z₀(w) qui serait mesurée si le tuyau était muni d'une terminaison non réfléchissante à l'autre extrémité. Cette impédance peut être réelle ou imaginaire, même sans amortissement dans le corps de l'instrument. Il n'est pas difficile de montrer alors que quand le tuyau est muni d'une terminaison quelconque (réelle, imaginaire ou complexe), l'impédance mesurée à l'entrée aura des valeurs maximum et minimum qui lui sont reliées de la façon suivante :

(Z_in)_max = [(1 + F)/(1 – F)]⁺¹                                             (35-17a)

(Z_in)_min = [(1 + F)/(1 – F)]^-1                                   (35-17b)

Ici le symbole F représente la fraction de l'amplitude du signal descendant qui revient à l'entrée après réflexion à l'autre extrémité. L'atténuation considérée ici est due à toutes les pertes subies dans un aller-retour dans le guide d'ondes, plus les pertes qui peuvent se produire pour une quelconque raison à l'autre extrémité. Il n'est pas possible de donner aussi simplement les fréquences auxquelles ces extrema se trouvent.

On voit clairement dans les équations 35-17a et 35-17b que dans bien des cas une mesure des maxima et minima de Z_in permet de déterminer Z₀(ω) - il suffit de calculer la moyenne géométrique de paires adjacentes de Z_max et Z_min. La courbe en pointillés sur les graphiques est une courbe moyenne qui représente le Z₀(ω) valable pour toutes les configurations de voyelles étudiées. Le fait que de telles configurations différentes partagent un comportement presque commun d'impédance d'onde est un fait intéressant et étonnant, dont nous pouvons extraire d'autres informations.

La théorie des tuyaux sonores nous indique que dans la limite des hautes fréquences, Z₀(w) tend vers une valeur qui est égale à l'impédance R₀ d'un guide d'ondes uniforme dont la section d'entrée est celle du tuyau. Les figures 35-6, 35-7 et 35-8 suggèrent sur la base de cette propriété que le PWW a une section d'entrée proche de celle d'un tuyau de 20 mm de diamètre intérieur (notre tête d'impédance est assez courte pour que sa propre section ne produise de complication dans aucune des interprétations que nous faisons sur la base de la théorie générale des tuyaux sonores).

Le fait que les pics et les minima des Z_u mesurées deviennent moins prononcés montre que les poumons (qui servent de terminaison du PWW) deviennent de moins en moins réfléchissants aux hautes fréquences. Ainsi, notre hypothèse initiale que le PWW montre peu ou pas de comportement résonnant est seulement justifiée dans la limite des hautes fréquences.

Nous pouvons utilement invoquer la théorie des tuyaux sonores pour faciliter l'extraction d'encore plus d'informations sur la nature acoustique du PWW. Si un tuyau a un cône à son entrée (de diamètre croissant ou décroissant), alors nous constatons que l'impédance de l'onde croît proportionnellement à la fréquence, depuis zéro à la fréquence nulle jusqu'à tendre vers la valeur de R₀ quand wx₀/c >> 1. Ici x₀ est la longueur du cône apical extrapolé à partir de la conicité initiale et de la section d'entrée du tuyau. Le fait que notre courbe déduite pour Z₀(w) reste au niveau de la valeur R₀ implique alors que notre PWW a très peu de conicité dans la région de la bouche (au moins dans les conditions de nos mesures !).

Une autre information globale peut encore être déduite d'une étude de nos courbes pour l'impédance d'entrée elle-même telle que mesurée pour le PWW. Si le PWW a une ouverture vers l'extérieur en un point quelconque sur sa longueur, alors Z_in a un zéro de premier ordre à la fréquence nulle. Si, d'autre part, le PWW est hermétique excepté à son extrémité d'entrée, l'impédance a un pôle simple à la fréquence nulle. C'est naturellement un truisme qui si l'instrument est muni d'une terminaison non réfléchissante, Z_in = Z₀(w) à la fréquence nulle (qui tend vers R₀). L'inspection des courbes de résonance des figures 35-6, 35-7, et 35-8 confirme donc que les poumons de l'instrumentiste fonctionnent comme une terminaison fermée et seulement légèrement réfléchissante pour le PWW.

Une information finale au sujet du PWW peut être obtenue en examinant la forme de son impédance d'entrée. C'est en fait l'aspect qui a immédiatement attiré mon attention quand les premières données ont été disponibles. Toutes les courbes d'impédance présentent une distribution des pics et des creux qui se superpose à une large bosse centrée au voisinage de 1000 hertz. Autrement dit, il y a une large bosse dans l'impédance de l'onde elle-même, et cette bosse est assez indépendante des autres détails de la structure du PWW. Cette sorte de modèle global rappelle le comportement générique de l'impédance d'entrée pour tous les doigtés des pistons d'un instrument de la famille des cuivres, dont l'explication est bien connue (Benade 1976, § 20.4, p. 400). Quand on prend en compte les autres implications systématiques de la forme du PWW comme décrit ci-dessus, on est conduit à suspecter qu'elle possède une constriction à peu de distance en amont, si bien que (très grossièrement) on trouve à l'entrée une sorte de résonateur de Helmholtz dont la fréquence naturelle est celle de la large bosse.

La figure 35-9 fournit la première preuve de la plausibilité de cette sorte de déduction. Ici nous voyons l'impédance d'entrée d'un morceau très long de tube de 20 mm de diamètre intérieur ayant une terminaison pratiquement.non réfléchissante. C'est-à-dire que nous avons une mesure directe de l'impédance d'onde Z₀(w). Le trait horizontal à travers le graphique vérifie qu'un tube uniforme a en fait une impédance mesurée indépendante de la fréquence de l'onde. La courbe supérieure montre la large bosse qui a été décrite dans le paragraphe précédent, qui est produite par l'introduction d'une constriction correctement proportionnée à une distance appropriée de l'entrée. Ces proportions peuvent être calculées à partir de la position et de la taille de la bosse, sans introduire d'autre paramètre pour tenir compte d'autres aspects de la courbe Z₀(w). Il y a une similitude agréable entre la forme de cette courbe et la courbe à main levée (vraisemblablement analogue) qui a été dessinée sur les courbes d'impédance ci-dessus.

La figure 35-10 montre l'impédance d'entrée d'un tube ouvert de 1900 mm de long dans lequel la même constriction est installée. La courbe Z₀(w) de la figure 35-9 est superposée pour montrer de façon synthétique à quel point les idées générales de la théorie des tuyaux sonores correspondent aux résultats expérimentaux. Les limites en fréquence haute et basse de Z_in et l'impédance de l'onde sont illustrées, avec le fait que sur un graphe en dB l'impédance de l'onde présente des pics et des creux. Le fait que dans le cas présent le tuyau est ouvert à l'air libre est indiqué par la faible valeur de l'impédance d'entrée aux basses fréquences.

La figure 35-11 est une illustration très semblable du comportement d'un guide d'ondes non-uniforme. Le seul aspect important dans lequel il diffère du précédent est la longueur hors-tout du tube, choisie cette fois proche de la longueur du PWW (telle que donnée à la figure 35-1). En dépit du fait que le tuyau est ouvert à l'autre extrémité, il est clair que la structure générale des pics et des creux rappelle fortement celle mesurée pour différentes configurations de voyelle du PWW. En particulier, l'espacement moyen des pics est identique, comme prévu pour des conduits unidimensionnels de longueur égale.

VI. SPECTRES MESURÉS

Nous considérerons d'abord les spectres mesurés des deux côtés de l'anche d'une colonne d'air de type clarinette ayant trois maximum d'impédance exactement alignés (situés aux multiples impairs de 240 Hz). Au-dessus de ceci (c.-à-d., au-dessus d'une fréquence de coupure du système de trous et de clés d'environ 1250 Hz), l'impédance se trouve près de la valeur caractéristique d'une ligne infinie de 15 mm de diamètre. Ceci signifie que la IAC elle-même peut produire de l'énergie fortement aux trois harmoniques impairs d'une fréquence jouée de 240 Hz. Le transfert hétérodyne d'énergie entre ces harmoniques constitue la source principale d'énergie dans l'oscillation globale. L'absorption d'énergie aux minima d'impédance situés à 480 et 960 Hz (multiples pairs de 240 Hz) et à toutes les fréquences harmoniques qui se trouvent au-dessus de la fréquence de coupure du système de trous et clés assure la stabilité d'amplitude.

Du côté amont de l'anche nous avons le PWW, dont la fonction d'impédance peut être aisément modifiée pour donner une grande variété de distributions de pics de résonance du type illustré sur les figures 35-6, 35-7, et 35-8 et discuté au paragraphe V. Pour le moment, il suffira de rappeler que le pic le plus haut de Z_u(w) tend à être deux ou trois fois plus élevé que le pic le plus haut de la courbe d'impédance de la IAC.

La discussion dans le paragraphe V a montré qu'on obtient une bonne oscillation régulière si l'impédance nette commandant l'anche a un ensemble de pics en relation harmonique. Nous n'avons pas à ce moment-là envisagé la question de ce qui arriverait au système si (comme dans le cas présent) l'impédance nette avait un ensemble de pics harmoniques plus un ou plusieurs inharmoniques, que l'on dira "non-conformistes". Nos expériences récentes montrent que (excepté dans des circonstances spéciales sur lesquelles nous reviendrons sous peu) un régime stable d'oscillation s'installe normalement sous la domination de l'ensemble des pics harmoniques. Ce régime d'oscillation "civilisé" implique la production énergétique à un ensemble de fréquences harmoniques de la façon déjà décrite, SANS PRODUCTION À LA FRÉQUENCE D'UN PIC NON-CONFORMISTE ! Cela a l'air un peu surprenant au début, mais si une sinusoïde devait être produite à la fréquence d'un pic non-conformiste, ses harmoniques produites non-linéairement, et les fréquences des produits d'intermodulation engendrés via le couplage non-linéaire aux composants harmoniques produits par ailleurs, se trouveraient en général aux points de la courbe globale d'impédance où elles fonctionneraient comme un énorme drain sur le budget d'énergie de l'oscillation globale. Il est donc clair que de telles oscillations ne sont pas normalement possibles. En conséquence nous constatons que la IAC domine la production de son de notre système expérimental, comme dans le cas d'une vraie clarinette, avec le PWW jouant un rôle auxiliaire de la façon que nous sommes sur le point de démontrer.


La moitié supérieure de la figure 35-12 montre le spectre du son (p_n)_d mesuré dans l'embouchure de notre IAC dans deux conditions expérimentales. La moitié inférieure de la figure montre les deux spectres correspondants (p_n)_u mesurés dans la bouche de l'instrumentiste. Les courbes en traits pleins dans les deux graphiques représentent les spectres mesurés dans la condition "normale" qu'aucune résonance du PWW n'est proche d'une résonance quelconque de la IAC. Le spectre a l'embouchure dans ces conditions est exactement de la forme qui nous est devenue familière dans notre travail sur les instruments à vent depuis de nombreuses années. Sa forme est commandée par l'impédance de la IAC, comme on a l'habitude de le tenir pour acquis (voir l'équation 35-8). Nous reconnaissons, maintenant, que l'invisibilité relative du PWW vient généralement du fait que ses résonances ne se situent pas normalement dans les endroits qui provoquent les circonstances spéciales visées ci-dessus, mais non encore explicitées. La courbe en traits pleins dans la partie inférieure de la figure, qui montre la nature du spectre correspondant dans la bouche de l'instrumentiste, n'a aucun aspect particulier sur lequel nous devrions insister pour le moment.

Si on écoute le signal pris par un microphone dans la bouche de l'instrumentiste pendant qu'il modifie la configuration de sa langue, etc., il est immédiatement évident qu'une ou l'autre des harmoniques de la note jouée est amplifiée très fortement quand elle est accordée avec une résonance du PWW. Les courbes en tirets dans les deux parties de la figure 35-12 montrent la nature du spectre observé quand le PWW a été configuré de sorte que la fréquence de son principal pic d'impédance coïncide avec la quatrième harmonique de la note jouée (à 960 hertz). Nous notons en premier lieu qu'il y a une augmentation de 40 dB (de 100 fois) de la force de cette harmonique dans la bouche de l'instrumentiste, avec un renforcement considérable de toutes les harmoniques voisines en raison de l'intermodulation entre ce composant fort et ses voisins.

Le spectre mesuré dans l'embouchure de notre "clarinette" quand le PWW est accordé harmoniquement (courbe en pointillés dans le diagramme supérieur) ne présente aucun changement particulièrement remarquable. Les amplitudes du fondamental et de la deuxième harmonique sont pratiquement inchangées, alors que la plupart des autres harmoniques sont renforcées de 5 ou 6 dB (un doublement d'amplitude). La quatrième harmonique, dont on pourrait penser qu'elle serait considérablement renforcée, a son niveau augmenté de seulement 12 dB (un quadruplement d'amplitude). Ces résultats illustrent et confirment le résultat mathématique décrit dans le paragraphe IV, à savoir que des modifications de Z_u et de Z_d montrent leurs effets prédominants du même côté de l'anche où les modifications ont eu lieu, avec seulement de petits changements discernables de l'autre côté.

On peut confirmer la faible importance perceptible des changements du signal dans l'embouchure en l'écoutant pendant la modification du PWW. On se rend compte seulement d'un changement plutôt subtil du son comme ce qu'on a l'habitude d'entendre quand un bon instrumentiste s'efforce d'obtenir le meilleur son. En d'autres termes, l'auditeur perçoit seulement un indice des changements drastiques qui se produisent dans la bouche de l'instrumentiste. Nous obtenons enfin une idée claire de ce qui se passe quand l'anche de clarinette collabore avec la IAC et le PWW. Nous commençons à comprendre comment le PWW pourrait jouer un rôle important d'une manière générale sans rendre jamais sa présence évidente. Par exemple, l'alignement approprié d'une résonance du PWW peut améliorer une note en stabilisant le régime d'oscillation et en réduisant le bruit parasite bien que son influence sur la couleur de son extérieurement perçue puisse être très faible.

Nous allons maintenant décrire les circonstances spéciales dans lesquelles le PWW peut faire sentir sa présence d'une manière manifeste. Considérons un système dynamique dans lequel la IAC est conçue pour donner un seul pic de résonance fort (dont on voit un exemple dans la partie plus inférieure de la figure 35-13, où le pic est à une fréquence f_a = 340 Hz). Si l'anche est alors commandée de son côté aval par une telle colonne d'air et de son côté amont par une certaine version du PWW, il n'y a aucun ensemble harmonique de pics de résonance qui peuvent coopérer pour installer un régime d'oscillation bien défini et le spectre harmonique correspondant. Si cependant l'instrumentiste explore les variations possibles de Z_u(w), il lui est possible de trouver un ou plusieurs cas où le pic le plus haut de la résonance du PWW se trouve à une fréquence f_b telle que la génération d'énergie à cette fréquence et à f_a soit suffisante pour alimenter tous leurs produits d'intermodulation, dont certains peuvent tomber sur un ou plusieurs des pics restants (répartis de façon inharmonique) de résonance du PWW. La partie supérieure de la figure 35-13 montre les spectres extrêmement compliqués dans l'embouchure et la bouche mesurés dans un tel cas spécial, dont le son est connu des musiciens pour être du type complexe entrelacé qu'ils appellent habituellement "multiphonique." De l'énergie vibratoire est produite principalement près de la fréquence du maximum d'impédance de la IAC et à un (ou peut-être plusieurs) des pics de résonance du PWW. En raison de la non-linéarité forte de l'anche, ces deux ou trois composants spectraux primaires ont engendré une foule de produits d'intermodulation. Nous avons réalisé de nombreuses versions de la configuration de la IAC et du PWW décrite ici, et nous pouvons toujours produire des sons multiphoniques exactement de la même manière. Dans tous les cas il a été possible d'analyser les spectres de la façon déjà établie pour le type analogue d'oscillation produit par une IAC dont les résonances sont inharmoniques (Benade 1976, chap. 25).

Il y a deux autres cas particuliers d'interaction IAC-PWW à considérer. Il se révèle facile de trouver des configurations du PWW dans lequel le plus haut des pics de résonance est situé de telle sorte que son couplage avec les résonances harmoniquement réparties de la IAC peut même perturber un régime établi d'oscillation harmonique et le remplacer par un multiphonique d'une complexité assez considérable. Les conditions dynamiques précises pour cette sorte de transition n'ont pas été établies jusqu'à présent, mais il s'avère qu'un instrumentiste peut, avec seulement une peu de pratique, apprendre à provoquer un tel multiphonique à partir de presque n'importe quelle note de sa gamme normale. Nous n'en dirons pas plus sur cette classe des phénomènes (qui nécessite considérablement plus d'étude), nous tournant à la place vers un cas particulier dynamiquement beaucoup plus simple, mais musicalement plus spectaculaire. Une solution a été trouvée au problème acoustique plutôt provocant de concevoir une IAC (pour utilisation avec un bec et une anche de clarinette) pour laquelle l'impédance d'entrée Z_d vue par l'anche est pratiquement non résonante (fondamentalement réelle) ; l'amplitude de cette impédance n'est pas plus du dixième environ de celle d'une perce normale de clarinette de 15 mm de diamètre. Clairement, une telle IAC ne peut donner aucune "instruction" au côté aval de l'anche, la laissant entièrement sous l'influence du PWW ! Des tentatives pour jouer sur cette colonne d'air sont rapidement récompensées par une variété de sons facilement contrôlables dont les hauteurs sont déterminées directement soit par la gamme des résonances de 450 à 1400 Hz facilement disponibles du PWW ou par la gamme de 2000 à 3000 Hz des fréquences de résonance de l'anche, où ZA peut être grand même lorsque Z elle-même n'est pas très renforcée aux hautes fréquences par le PWW. Dans le premier cas, des mouvements de langue de l'instrumentiste, etc., modifient la hauteur de son, avec très peu d'influence des variations de la pression des lèvres qui commande la fréquence de résonance de l'anche elle-même. Dans l'autre cas, la fréquence de jeu dépend presque exclusivement de la tension des lèvres (via la fréquence propre de l'anche). Elle ne montre aucune influence des résonances (à basse fréquence) du PWW qui sont commandées par la configuration du tractus de l'instrumentiste. L'auditeur identifie très facilement lequel des deux modes du jeu est en action, et détecte le passage de la prépondérance de l'un à l'autre quand l'instrumentiste parvient à pousser l'un d'entre eux vers le domaine du jeu facile de l'autre.

Il est vite évident qu'un bon joueur d'instrument à anche n'a aucun mal à apprendre à contrôler les résonances de son PWW pour des buts quasi musicaux. Je possède un enregistreur à cassettes sur lequel ont été enregistrés au microphone des signaux des côtés amont et aval de l'anche tandis que George Jameson exécutait (sur demande, en succession rapide, et pratiquement sans entraînement) une grande variété d'extraits musicaux familiers, parmi lesquels les thèmes du concerto pour trompette et de la symphonie "La surprise" de Haydn", du concerto pour clarinette de Mozart, du Sextuor de "Lucia di Lammermoor", et de "Cœurs et Fleurs." Dans tous les cas la maîtrise de l'exécution et de la justesse était au moins égale à celle de n'importe quel siffleur amateur doté d'une bonne oreille. Notez surtout que je NE VEUX PAS dire que la facilité avec laquelle ce nouveau mode d'exécution a été appris démontre que cette façon de jouer est parallèle à celle qui est bien connue d'un instrumentiste dans la pratique professionnelle normale de son instrument ! Tandis qu'il peut s'avérer en être ainsi après que nous ayons effectué une étude appropriée de la question, nous devrions nous rappeler à ce stade que le même instrumentiste aurait probablement aussi bien joué sur un jazzoflûte ou une scie musicale (qui exige les habiletés motrices qui lui sont vraiment peu familières).

VII. CONCLUSION

Pour le moment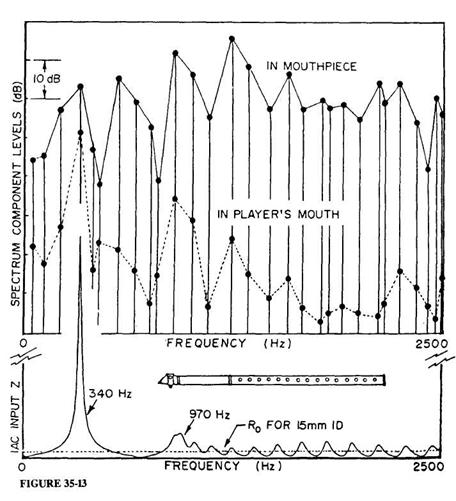 nous nous contenterons de la connaissance que l'anche s'est montrée parfaitement disposée à obéir aux résonances de ses côtés amont ou aval. Nous avons également appris que les résonances en relation harmonique des deux côtés de l'anche peuvent travailler ensemble pour donner un son régulier et propre ; qu'une résonance (inharmonique) non-conformiste ne dérangera pas habituellement le fonctionnement normal de l'anche commandée par un ensemble de résonances en relation harmonique ; et que, dans des circonstances particulières, elle peut perturber l'oscillation, produisant à la place un son multiphonique d'une complexité considérable.

Dans la mesure où nos investigations musicales ont progressé, nous avons de bonnes raisons de croire que la plupart des joueurs d'instruments à anche (mais pas tous) utilisent actuellement les résonances de leur PWW pour "remplir", "clarifier" ou "ajuster" les notes qu'ils jouent. Parmi les joueurs de cuivres, un tel comportement semble beaucoup plus répandu. Quoi qu'il en soit, nous commençons à comprendre la relation entre les recommandations traditionnelles des professeurs d'instrument et les positions des diverses résonances dans le PWW. Nous sommes également forcés de bien reconnaître que la nature de ces relations n'a pas été facilement prévue par le physicien. En particulier, nous devons nous rappeler qu'il est tout à fait absurde de prévoir, a priori, que les positions des fréquences des formants de voyelles ont un lien direct avec les maxima d'impédance du PWW comme nous l'avons montré. C'est parce que les résonances du PWW qui nous intéressent sont associées aux modes normaux d'une colonne d'air ayant une impédance élevée (c.-à-d., un tuyau fermé du côté de la bouche de l'instrumentiste et une terminaison compliquée à l'autre extrémité constituée par les poumons, tandis que les fréquences des formants de voyelles appartiennent à une colonne d'air (beaucoup plus courte) qui a une terminaison à basse impédance côté bouche et à haute impédance (pratiquement fermée) côté larynx !

En conclusion je résumerai l'ensemble de cet article en indiquant les raisons pour lesquelles les effets de la colonne d'air de l'instrumentiste sont arrivés à rester hors du champ d'investigation scientifique pendant si longtemps. Tout d'abord, tout instrumentiste apprend presque immédiatement les actions faciles permettant d'éviter les configurations "pathologiques" du PWW qui provoquent les sons multiphoniques qui peuvent se produire en dépit de la présence des résonances alignées de la IAC ; ces sons peuvent être identifiés comme les "couinements" souvent produits par les débutants.

Deuxièmement, les effets audibles de l'alignement des résonances dans le PWW sont plutôt subtils et pas aisément reconnus dans le spectre de l'embouchure de l'instrument ou dans celui qu'il engendre dans la salle de concert. Comme nous l'avons vu, leur existence n'a été vraiment démontrable qu'une fois que nous avons commencé à avoir une vue globale. Bien d'autres subtilités de couleur et de réponse de son ont dû être identifiées et expliquées (si non mesurées) avant que les effets du PWW aient pu être clairement étudiés.

Une troisième raison, bien que tout à fait personnelle à l'auteur, est tout à fait typique de la cause de beaucoup de recherches en acoustique musicale. Au début de mes études d'acoustique, je jouais assez bien de beaucoup d'instruments à vent, suffisamment pour avoir un peu confiance en mes jugements sur le son, la justesse et la réponse et leurs implications dynamiques (toujours sujets à révision par les commentaires des instrumentistes professionnels et par les données acquises au laboratoire). Cette connaissance des instruments m'a aidé à concevoir des expériences de vérification, et à noter les phénomènes qui pourraient ou ne pourraient pas mériter une étude plus approfondie. Mais j'ai dû mettre de côté la prise en compte formelle des paramètres physiologiques au profit des questions plus accessibles de physique. Dans cet esprit et sous l'influence des écrits de Bouasse, nous avons poursuivi à Cleveland l'idée d'aligner les résonances de la IAC et avons porté la physique assez loin pour guider ma production de clarinettes, de flûtes et d'autres instruments musicalement intéressants (conçus pour satisfaire mon propre goût, après quoi ils ont généralement obtenu l'approbation d'instrumentistes distingués). Pendant plusieurs années, je ne me suis pas rendu compte que j'exploitais le phénomène de résonance d'anche via des variations de tension des lèvres en jouant pendant que j'ajustais physiquement les instruments. Rétrospectivement, je me rends compte de la chance que j'ai eue que mes principaux conseillers musicaux pour la famille de la clarinette, scientifiquement la plus accessible, aient été tous de la vieille école, et aient eu l'habitude d'utiliser ces résonances dans leur propre jeu, de sorte que mes efforts inconscients n'ont pas été contredits ni embrouillés par les commentaires de mes conseillers. (Cette ressource s'avère maintenant exploitée par une partie seulement des joueurs de clarinette plus jeunes, en partie parce que les instruments commerciaux d'aujourd'hui sont construits de telle manière que ce genre d'exploitation soit difficile voire impossible). L'exploitation du phénomène de résonance d'anche est pratique normale pour les autres instruments. Quoi qu'il en soit, une fois que les phénomènes de coopération ont été bien acquis, il a été possible d'y rattacher la physique des effets de résonance d'anche (Thompson 1979) et de relier ces derniers à la technique musicale. Pendant ce temps, mes amis musiciens continuaient à insister sur le fait que la tension des lèvres était nullement le seul moyen de commande physiologique à la disposition de l'instrumentiste et, dès le début, j'ai eu le sentiment qu'ils avaient raison. A mesure que je m'améliorais comme instrumentiste, je devenais de plus en plus conscient des possibilités et aussi de plus en plus certain (comme d'autres choses se mettaient en place) que le moment approchait où on allait pouvoir en faire une étude valable. Le parallèle intellectuel entre le PWW et les études de résonance d'anche a été identifié et utilisé comme un encouragement. Auparavant, il a fallu une certaine désinvolture pour laisser purement et simplement quelque chose de côté jusqu'à ce qu'elle s'impose à notre vue !

La morale de l'histoire est que les progrès en acoustique musicale sont accomplis (mieux ? seulement ?) par un genre spécial de créature à deux jambes : une de ses jambes nécessaires est scientifique, alors que l'autre est musicale, et il est important que les deux soient solides et en bon état de marche.

Étude réalisée avec l'aide d'une subvention de la National Science Foundation.

RÉFÉRENCES

Backus, J. (1962). "Small vibration theory of the clarinet," J. Acoust. Soc. Am. 35, 301.
Benade, A.H. (1976). Fundamentals of Musical Acoustics.Oxford Univ. Press, New York.
Bouasse, H. (1920-30). Instruments à Vent. 2 Vols. Librarie Delagrave, Paris, I:115-116, 312-314, II:47.
Dawson, S.V. (1976). "Input impedance measurements of the respiratory system by impulse response," Tech. Prog. Rep. Harvard School of Public Health.
Fransson, F. (1965-75). A series of articles on the STL ionophone transducer published in the STL QPSR, Stockholm.
Fransson, F. and Jansson, E. (1975). "The STL ionophone transducer, properties and construction," J. Acoust. Soc. Am. 58, 910.
Ibisi, M.I. and Benade, A.H. (1982). "Impedance and impulse response measurements using low-cost components," J. Acoust. Soc. Am. 72, S63.
Krüger, W. (1979). "The impulse method of determining the characteristics of brass instrument response," Proc. of the Musical Acoust. Conf. (in German). Cesky Krumlov (Sept. 1979). Reprinted (in Czech) in Hudebni Nastroje 17, 52 (1980).
Oliver, B.M. (1964). "Time domain reflectometry," Hewlett-Packard J. 15/1. See also HP Application Note 75 "Selected articles on TDR applications.
Rosenberg, J. and Gordon, H. (1966). "The pulsed acoustic reflectometer," Physics Lab. Proj. Rep. Case Institute of Tech., Case Western Reserve Univ.
Thompson, S.C. (1978). "Reed resonance effects on woodwind nonlinear feedback oscillations," doctoral diss., Case Western Reserve Univ.
Thompson, S.C. (1979). "The effect of reed resonance on woodwind tone production," J. Acoust. Soc. Am. 66, 1299.

DISCUSSION

P. MILENKOVIC : Les professeurs de flûte vous disent également de faire des choses avec la bouche. Avez vous une idée sur la façon d'aborder ce problème avec les flûtes ?

A. BENADE : Les effets de cette sorte sont très, très faibles dans les flûtes. J'ai dit un certain nombre de choses au sujet de l'influence de la bouche [A.H. Benade et J.W. French J. Acoust. Soc. Am. 37, 679, 1964], qui sont erronées. Et John Coltman a dit des choses [J. Acoust. Soc. Am. 54, 417, 1973] que je crois maintenant pas tout à fait exactes. Elles ne sont pas fausses. Ces effets sont très petits parce que c'est longitudinal. Ils ont une importance, naturellement. Maintenant je peux repèrer comment un flûtiste a placé sa bouche en l'écoutant. Les musiciens avec qui nous en avons parlé diffèrent au sujet d'un effet très léger comparé à celui dont je traite ici. [Preuve supplémentaire : Walther Krüger du DDR a récemment montré des effets importants sur une flûte à bec].

M. ROTHENBERG : Je ne peux m'empêcher de poser cette question parce je l'ai en tête depuis tellement longtemps. Il y a quelques années j'ai fait quelques expériences avec un harmonica. Avez vous jamais travaillé avec cet instrument ?

A. BENADE : Par hasard j'ai reçu une lettre posant pratiquement cette même question de Roy Childs de la Société Américaine d'Harmonica presque juste au moment où tout ceci commençait à occuper mon esprit d'une manière sérieuse. L'anche de l'harmonica est nominalement du type "libre" avec sa propre fréquence de vibration. En élaborant la théorie de façon très semblables à celle décrite dans cet article, on montre (et l'expérience le confirme) que l'oscillation est seulement possible quand il y a un certain inertie dans le conduit de l'air, et que la fréquence de vibration peut être bougée en changeant la part de résistance visqueuse (réelle) dans l'impédance du conduit.

M. ROTHENBERG : J'ai entendu une fois quelqu'un jouer de l'harmonica dans un magasin de musique, faisant toute cette belle musique. Et je savais jouer "Oh Susannah!", vous savez. Aussi je me suis approché ; je m'attendais à voir un engin colossal avec toutes sortes de boutons, mais il avait un petit harmonica de marin. Aussi j'ai pris réellement un cours, avec un ami à moi qui joue de l'harmonica, et j'ai découvert qu'on pouvait forcer la vibration de l'anche. En outre, mes expériences en soufflant dans l'harmonica de l'air comprimé, et en utilisant une charge acoustique réglable derrière l'embouchure, m'ont également convaincu qu'une grande partie de la belle musique qu'un bon instrumentiste peut obtenir à partir d'un petit harmonica simple est due principalement à la charge acoustique de l'anche obtenue en formant convenablement les lèvres, le tractus et le larynx. Cependant, bien que j'aie vécu dans le tractus, pour ainsi dire, pendant environ 15 ans, et que j'aie, je crois, une bonne compréhension de ce que les manipulations du tractus pourraient causer comme changements cruciaux de charge acoustique au niveau des lèvres, après environ 10 heures d'instruction experte, j'arrivais seulement à exécuter les exemples les plus faciles d'"anche forcée" (que je définirais comme un décalage de hauteur de son de l'anche censément inactive qui s'y oppose).

A. BENADE : Eh bien, voici quelque chose qui distrait des personnes comme nous. La partie réelle de Z parle ici à la partie imaginaire de l'anche et vice versa dans beaucoup de ces situations. Et en tirant ainsi la fréquence, cela qu'on peut faire en mettant un mouchoir ou quelque chose en travers de la colonne d'air, on peut la déplacer pas mal. Nous avons des réflexes rétrogrades ici. Merci de soulever la question parce que j'avais eu l'intention de me pencher un peu sur les questions de Roy Childs. Un harmoniciste irlandais m'a également rendu visite, ce qui m'a un peu stimulé.

* JASA = Journal of the Acoustic Society of America

Traduit en mars 2004 par Joël Eymard pour le site web "Tout sur la trompette" avec l'autorisation de Virginia Benade