 Figure 1. Systèmes de mesure et d'étalonnage des
différences de phase : (a) microphone de mesure et jauge de
contrainte pour détecter la pression dans l'embouchure et la
contrainte de la lèvre, respectivement, (b) installation
d'étalonnage pour fournir une référence de la
différence de phase de 180° entre la pression et les signaux
de contrainte, et (c) canaux dynamiques de pression et de contrainte
pour la mesure de différence de phase.
Figure 1. Systèmes de mesure et d'étalonnage des
différences de phase : (a) microphone de mesure et jauge de
contrainte pour détecter la pression dans l'embouchure et la
contrainte de la lèvre, respectivement, (b) installation
d'étalonnage pour fournir une référence de la
différence de phase de 180° entre la pression et les signaux
de contrainte, et (c) canaux dynamiques de pression et de contrainte
pour la mesure de différence de phase. |
Un système pour mesurer la différence de phase entre
la pression acoustique dans une embouchure et le déplacement
vibratoire de la lèvre supérieure est esquissé
à la fig. 1(a) et (c). Une jauge de contrainte (type
B-FAE-05W-12 de Shinkoh) a été étroitement
fixée à la lèvre supérieure par un morceau
de ruban adhésif double face (Nichiban, Celtack CW-18). Cette
jauge est très petite (0,5 millimètre de long et 1,2
millimètre de large) et n'a pas entravé la
flexibilité de la lèvre même pour jouer du cor et
de la trompette. La jauge, traitée comme une résistance
électrique, est reliée par un conducteur court à
un circuit en pont (modèle Kyowa DB-120P) qui est
équilibré quand aucune contrainte n'est appliquée.
La contrainte appliquée est lue comme une tension
électrique, qui apparaît comme un écart par rapport
à l'équilibre. Ce signal est amplifié par un
amplificateur dynamique de contrainte (modèle Kyowa DMP-611,
avec un filtrage passe-bas appliqué à 1 kHz) et par un
amplificateur additionnel (modèle 451 d'Ithaco). Le signal
amplifié est envoyé à un enregistreur
numérique de forme d'onde sur 12 bits (modèle 5183 de
Hewlett-Packard).
La pression acoustique dans une embouchure (ou à l'entrée
d'un tube sans embouchure) est prise par un microphone de mesure (type
4182 de Brüel et de Kjaer), qui est relié à un
amplificateur (type 2609 de B&K). La sonde du microphone a une
longueur de 25 mm et un diamètre interne de 1,24
millimètre. Le signal amplifié est alors envoyé
à un autre canal de l'enregistreur de forme d'onde ci-dessus.
Finalement, la pression et les signaux de contrainte, qui sont
simultanément mesurés, sont transformés en
spectres de phase dans le domaine des fréquences. La
différence de phase Lp – Lε est obtenue en soustrayant le spectre de phase de la contrainte dynamique Lε de celui de la pression acoustique Lp et en lisant la valeur à la fréquence jouée.
Avant de mesurer les différences de phase dans les quatre
systèmes acoustiques mentionnés dans l'introduction, on a
brièvement examiné l'applicabilité de la technique
de détection de contraintes pour la vibration des lèvres.
Les lèvres sont mises en vibration (c'est le "buzzing") quand de
l'air est soufflé entre les lèvres initialement
fermées. L'auteur a mesuré avec une jauge de contrainte
une telle vibration auto-entretenue de ses lèvres et a obtenu le
résultat suivant : les vibrations stables des lèvres
avaient une fréquence fondamentale comprise entre 25 et 48 Hz
avec une structure harmonique très riche atteignant
jusqu'à la 17ème-21ème
harmonique, où le niveau du signal se confondait presque au
niveau du bruit. La gamme dynamique de notre système de mesure
de contrainte a été alors estimée à plus de
40 dB quand le filtrage passe-bas a été appliquée
à 1 kHz. Ce résultat a prouvé l'efficacité
de la détection de contrainte pour mesurer la vibration des
lèvres d'un joueur de cuivres.
B.
Méthode d'étalonnage des différences de phase
Le calibrage pour déterminer la différence de phase entre
pression et contrainte montré sur la fig. l(c) a
été effectué en utilisant l'installation
présentée à la fig.1(b). Un tel calibrage est
nécessaire pour définir la différence de phase
nulle. La même jauge de contrainte qu'utilisée pour la
détection des mouvements des lèvres à la fig. 1(a)
a été fixée au centre d'un petit haut-parleur en
forme de dôme (modèle Phillips 544) de la manière
décrite à la section I A. La pression acoustique a
été mesurée juste devant ce diaphragme en
utilisant le même microphone de mesure montré sur la
fig.1(a).
L'étalonnage est fondé sur l'hypothèse que la
contrainte du diaphragme et la pression résultante à
proximité doivent être en opposition de phase. Puisque le
diaphragme peut être considéré comme une source
simple (monopôle) dans la gamme des basses fréquences qui
nous intéresse, la pression à proximité p(r) est proportionnelle à l'accélération radiale30 et peut être reliée au déplacement radial ξ d'une source monopolaire selon l'équation :
p(r) / ξ = –ω2ρS / 4πr,
où r est la distance de la source, S la surface de la source, ω est la pulsation et ρ
la densité de l'air. On peut raisonnablement supposer aussi
qu'aux basses fréquences, où le mouvement du diaphragme
est entièrement en phase, la contrainte interne est
proportionnelle au déplacement radial. Ces hypothèses
permettent de conjecturer que la contrainte du diaphragme et la
pression résultante à proximité sont en opposition
de phase.
Il en résulte que le montage présenté à la
fig.1(b) établit une référence de la
différence de phase 180° entre les signaux de pression et de
contrainte. La différence de phase Φ entre les deux canaux de la fig. 1(c) est ainsi estimée comme :
Φ = (Lp – Lε)CAL – 180°, (1)
où (Lp – Lε)
indique la différence de phase mesurée par la
méthode de calibrage ci-dessus basée sur les fig. l(b) et
(c).
C.
Relation entre la contrainte et le déplacement de la lèvre supérieure
Nous devons déterminer la relation entre la contrainte et le
déplacement de la lèvre supérieure parce que nous
avons besoin de la différence de phase calibrée entre la
pression d'embouchure et le déplacement de la lèvre. Il
faudrait étudier la mécanique des tissus musculaires
comme l'ont développée Titze et Talkin11
pour différentes configurations des cordes vocales pour obtenir
une relation quantitative entre contrainte et déplacement pour
différentes configurations de lèvre. C'est toutefois un
problème à traiter dans le futur. Pour le moment il nous
suffit d'avoir la relation de phase quand l'instrument joue.
Supposons que la lèvre supérieure se compose d'une masse
et d'un ressort dont l'extrémité supérieure est
fixe à une position correspondant au bord de l'embouchure. Ce
ressort de lèvre est comprimé et étiré ; la
masse de lèvre subit une force de rappel quand la lèvre
est écartée de sa position d'équilibre. Quand le
ressort est comprimé, les lèvres tendent à
s'ouvrir avec un déplacement positif de la lèvre
supérieure (vers le haut ou vers l'extérieur). Le ressort
ainsi comprimé provoque une contrainte négative sur le
bord de la lèvre. Quand le ressort est étiré, les
lèvres tendent à se fermer avec un déplacement
négatif de la lèvre supérieure. Le ressort ainsi
étiré provoque une contrainte positive sur le bord de la
lèvre. En conséquence, nous pouvons en déduire que
la contrainte et le déplacement de la lèvre
supérieure sont en opposition de phase. En outre, si on
considère le buzzing, on peut comprendre que la lèvre
inférieure favorise cette relation d'opposition de phase. Quand
la lèvre supérieure heurte la lèvre
inférieure, l'impulsion de pression fournie par la lèvre
inférieure donne à la lèvre supérieure un
effort négatif et un déplacement positif pour rouvrir les
lèvres juste après la collision. Puisqu'un effort
négatif sur le bord de la lèvre donne une contrainte
négative, la relation d'opposition de phase mentionnée
ci-dessus est renforcée. Quand la lèvre supérieure
s'écarte de la lèvre inférieure, la dynamique des
lèvre est commandée par la force de rappel interne. La
relation d'opposition de phase est toujours une hypothèse qui
nécessite d'autres éclaircissements.
Par conséquent nous avons la relation suivante
:
(Lp – Lξ)MEAS = (Lp – Lε)MEAS – 180°, (2)
où ξ et ε sont respectivement le déplacement et la contrainte de la lèvre. En outre, ( )MEAS
désigne la valeur obtenue par le système de mesure
présenté aux fig. l(a) et (c). La différence de
phase vraie est ainsi dérivée des équations (1) et
(2) comme suit :
Lp – Lξ = (Lp – Lξ)MEAS – Φ = (Lp – Lε)MEAS – (Lp – Lε)CAL (3)
Les valeurs (Lp – Lε)CAL
définissent une courbe de "différence de phase nulle",
dont des exemples seront montrés dans la section I D.
Notre méthode de détection des contraintes dans le
comportement des lèvres nécessite quelques commentaires.
Selon Martin4,
les mouvements ascendants et extérieurs de la lèvre
supérieure sont presque en phase et forment une ouverture.
D'ailleurs, l'aire d'ouverture de lèvre est approximativement
proportionnelle à l'écartement central qui est
principalement du au mouvement ascendant de la lèvre
supérieure. Par conséquent nous pouvons considérer
que le mouvement ascendant est plus significatif que le mouvement vers
l'extérieur. Cela ressort également de la comparaison
entre les figures 4 et 5 dans la réf. 4. En fait, on obtenait un
signal de sortie plus important de la jauge de contrainte quand elle
était fixée dans une position plus intérieure de
la lèvre supérieure. Mais la jauge avait tendance
à sortir en raison de l'humidité dans la bouche et de la
circulation d'air le long de la surface de la lèvre. Aussi la
jauge a été fixée à une position
appropriée, pas trop profondément, pas trop
extérieure, de sorte qu'elle puisse durer au moins quelques
heures pour l'expérience. Fixée à une position
appropriée, la jauge était bien visible dans un miroir en
prenant la configuration d'embouchure pour jouer des instruments. Par
conséquent la jauge de contrainte peut détecter le
mouvement vers l'extérieur comme le mouvement ascendant, bien
que le rapport des sensibilités à ces mouvements ne soit
pas connu. En outre, la lèvre supérieure est
considérée comme le principal vibrateur4,31,32, en particulier aux fréquences les plus élevées.
 Figure
2. Différence de phase entre la pression acoustique et la
contrainte dynamique dans le système d'étalonnage des
fig. l(b) et (c). L'axe des ordonnées de gauche et des abscisses
du haut (de 100 à 450 Hz) se rapportent aux jauges Bl et B2.
L'axe des ordonnées de droite et des abscisses du bas (de 280
à 315 Hz) se rapportent à la jauge A. Figure
2. Différence de phase entre la pression acoustique et la
contrainte dynamique dans le système d'étalonnage des
fig. l(b) et (c). L'axe des ordonnées de gauche et des abscisses
du haut (de 100 à 450 Hz) se rapportent aux jauges Bl et B2.
L'axe des ordonnées de droite et des abscisses du bas (de 280
à 315 Hz) se rapportent à la jauge A. |
D. Courbe de différence de phase nulle
Les valeurs mesurées de (Lp – Lε)CAL, qui définissent la différence de phase nulle utilisée pour évaluer (Lp – Lξ) selon l'éq. (3), sont montrés dans la fig. 2. Les réponses des jauges Bl et B2, qui incluent des conducteurs additionnels de 77 centimètres et 60 centimètres, respectivement, ont été mesurées avec le système décrit dans la section I A. D'autre part, la réponse de la jauge A, qui inclut un fil d'approximativement 100 centimètres, a été mesurée avec un autre système se composant d'un circuit en pont fabriqué à la main, d'un amplificateur (modèle 451 d'Ithaco) et d'un filtre passe-bande (modèle N-F FV-625A) dont la largeur de bande a été réglée à 100 Hz. En outre, un petit microphone à électret a été utilisé au lieu du microphone de mesure pour mesurer la différence de phase avec la jauge A. Ce système un peu bricolé a été appliqué à un tube excité par les lèvres sans embouchure8, et les résultats expérimentaux sont décrits dans la section II A.
Les courbes d'étalonnage pour les jauges B1 et B2 montrées à la fig. 2 indiquent que la différence de phase entre les canaux de pression et de contrainte a la même dépendance par rapport à la fréquence, bien que la cause de la petite différence d'amplitude entre eux ne soit pas expliquée. Le fil très fin (28 mm de long) sortant de la jauge elle-même n'était pas très solide, et a été parfois cassé par l'effort entre le bord de l'embouchure et la lèvre supérieure. À cette occasion la jauge cassée a été remplacée par une neuve, mais la mesure (Lp – Lε)CAL n'a pas été refaite. Les trois courbes dans la fig. 2 sont utilisées pour définir la différence de phase nulle dans la section II.
II. RÉSULTATS EXPÉRIMENTAUX
A. Tube résonant sans embouchure
 Figure 3. Différence de phase (Lp – Lε)MEAS dans des tubes excités sans embouchure : (a) tube 1, avec la jauge A, (b) tube 3, avec la jauge B2. Symbole • : lèvre supérieure relativement mince étirée en longueur, o : lèvre supérieure relativement détendue et rentrant dans le tube. |
Les figures 3(a) et (b) montrent les résultats sur le tube 1 et le tube 3, respectivement. La distribution expérimentale des données dans la figure 3(a) se divise clairement en deux groupes : un groupe a de plus basses fréquences et des différences de phase positives [nous considérons le Lp – Lξ dans l'éq. (3)] ; l'autre a des fréquences plus élevées et des différences de phase négatives. Un résultat très semblable a été dérivé du tube 2 plus grand. D'autre part, la fig. 3(b) se compose presque de seulement un groupe avec des différences de phase positives. Le groupe des différences de phase négatives peut corroborer le modèle de vibration de lèvre vers l'extérieur, alors que le groupe des différences positives est incompatible avec ce modèle, mais suggère un modèle à une masse de vibration verticale des lèvres33.
On a pu produire des fréquences de son plus élevées donnant des différences de phase négatives en étirant les lèvres serrées et en rendant la lèvre supérieure tendue et mince (cf. symbole • dans la fig. 3). Mais on a produit des fréquences plus basses donnant des différences de phase positives, en détendant les lèvres et en faisant dépasser la lèvre supérieure (cf. symbole o dans la fig. 3). La configuration de jeu dépend de la flexibilité des lèvres, qui dépend à son tour du diamètre du tube sur lequel elles s'appuient. Ce diamètre influence la liberté vibratoire. Une telle interdépendance doit être complexe et subtile parce que la différence entre 3(a) et (b) vient d'une petite différence de diamètre de tube entre le tube 1 et le tube 3.
Comme l'analyse de cette interdépendance est difficile, nous devons limiter nos conclusions à ce qui suit : Les expériences avec les tubes les plus grands (1 et 2) confirment les modèles de vibration vers l'extérieur et de vibration verticale de la lèvre ; le tube plus petit (3) soutient à peine le modèle de vibration de la lèvre vers l'extérieur. La validité de ce jugement et notre méthode de mesure de différence de phase décrite dans la section I seront reconfirmées dans la section III B par la relation entre la fréquence jouée et la fréquence de résonance propre de l'instrument.
B. Tube non résonant avec une embouchure
Beaucoup de joueurs de cuivre ont un tube pour pratiquer silencieusement le "buzzing" et exercer leur contrôle des lèvres dans une embouchure. La figure 4 montre ce tube de travail avec une embouchure de cor (Lawson S660) ainsi qu'une jauge de contrainte, un circuit en pont, un microphone de mesure et les tubes résonants avec une embouchure (voir la section II C). Le tube de travail comprend les 18 premier centimètres (coniques) d'une branche d'embouchure de cor fixés à un court tube cylindrique fermé avec un grand trou latéral. En ajustant la taille de l'ouverture de trou, l'instrumentiste peut contrôler la "résistance" pendant la pratique. Ce tube inhibe toutes les harmoniques jouables, mais laisse assez de rétroaction pour donner au joueur une sensation semblable à celle de son instrument. Dans ce sens ce tube est non résonant28,29 et peut donc être utilisé pour examiner le comportement de la lèvre dans une embouchure sur une grande plage de fréquence.
Le résultat expérimental présenté fig. 5 montre que la différence de phase Lp – Lξ de l'éq. (3) a des valeurs négatives de –10° à –40° excepté pour quelques points. En raison du caractère non résonant du système embouchure – tube, la fréquence jouée varie dans une large plage de 250 à 445 Hz au lieu de la bande étroite montrée dans la fig. 3 pour le tube résonant excité avec les lèvres. On a également obtenu des résultats semblables en utilisant une embouchure de trompette (Bach 5C) au lieu d'une embouchure de cor. Les valeurs négatives de la différence de phase suggèrent que la lèvre supérieure fonctionne en mode de vibration vers l'extérieur avec un système embouchure – tube non-résonant.
C. Tube résonant avec une embouchure
 Figure 4. Ensembles tube non résonant – embouchure et tube résonants – embouchure, (a) embouchure de cor (Lawson S660), (b) tube non résonant d'entraînement, (c) jauge de contrainte, (d) circuit en pont, (e) microphone de mesure, (f) embouchure de trompette (Bach 5C), (g) tube résonant Rl, et (h) tube résonant R2.  Figure 5. Différence de phase entre la pression acoustique p dans l'embouchure et la contrainte ε
de la lèvre quand on émet un son avec un système
embouchure – tube non résonant (voir la fig. 4). o :
Données mesurées pour un tube bouché à
l'extrémité. •:
Données mesurées pour un tube non bouché. La jauge
B1 a été utilisée pour la détection de
contrainte. Figure 5. Différence de phase entre la pression acoustique p dans l'embouchure et la contrainte ε
de la lèvre quand on émet un son avec un système
embouchure – tube non résonant (voir la fig. 4). o :
Données mesurées pour un tube bouché à
l'extrémité. •:
Données mesurées pour un tube non bouché. La jauge
B1 a été utilisée pour la détection de
contrainte.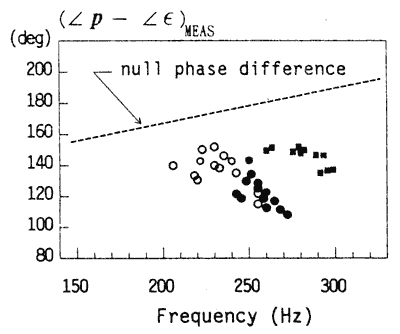 Figure 6. Différence de phase mesurée entre la pression acoustique p
dans l'embouchure et la contrainteε de la lèvre du
joueur avec les systèmes acoustiques suivants : o,
système embouchure de trompette – tube résonant Rl,
•, système embouchure de
cor – tube résonant R1, et D, système embouchure de
cor – tube résonant R2. La jauge B2 a été
utilisée pour la détection de contrainte. Figure 6. Différence de phase mesurée entre la pression acoustique p
dans l'embouchure et la contrainteε de la lèvre du
joueur avec les systèmes acoustiques suivants : o,
système embouchure de trompette – tube résonant Rl,
•, système embouchure de
cor – tube résonant R1, et D, système embouchure de
cor – tube résonant R2. La jauge B2 a été
utilisée pour la détection de contrainte. |
Comme les résultats expérimentaux du système
embouchure – tube non résonant semblent montrer seulement
un comportement des lèvres qui "buzzent" sans rétroaction
acoustique significative, il faut faire des expériences
additionnelles sur un système embouchure – tube
résonant.
On a pris deux types de tube en laiton (voir fig. 4) : le tube Rl
était de 350 mm de long avec un diamètre intérieur
de 7mm sauf du côté d'un récepteur d'embouchure de
15 mm avec un diamètre intérieur de 7,8 mm ; le tube R2
est de 300 mm de long avec un diamètre intérieur de 21 mm
sauf du côté d'un récepteur d'embouchure de 41 mm
dans lequel la géométrie intérieure passe de
cylindrique (15 mm de long et 7,8 mm de diamètre
intérieur) à conique tronqué (26 mm de long). Ces
tubes sont bien adaptés à une embouchure de cor. Comme
l'embouchure de trompette a une queue plus grosse que celle de cor, un
raccord approprié est inséré entre l'embouchure de
trompette et le tube.
Les résultats expérimentaux présentés fig.
6 indiquent que les trois couples (embouchure de trompette – tube
R1, embouchure de cor – tube R1 et embouchure de cor – tube
R2) montrent des différences de phase négatives Lp – Lξ
allant d'environ –20° à environ –70°. Ceci
suggère que le modèle de lèvre vibrant vers
l'extérieur est valable même dans les systèmes
embouchure – tubes résonants. De plus, comme décrit
dans la section III B, la fréquence de résonance
calculée du système embouchure – tube
résonant est clairement inférieure à la
fréquence jouée comme le montre la fig 6. Cette relation
de fréquence confirme la fiabilité de la relation de
phase de la fig. 6 et la prédominance du modèle de
lèvre vibrant vers l'extérieur. Cependant, il convient de
noter que ce résultat expérimental est limité
seulement au mode fondamental parce que l'excitation des
résonances plus élevés était trop difficile.
En outre, il faut noter que les systèmes embouchure –
tubes résonants ont une bande de fréquence de
résonance beaucoup plus large que les tubes excités par
les lèvres sans embouchure. La largeur de bande de
résonance des uns est de 30-40 Hz comme on le voit fig. 6, alors
que celle de ces derniers est d'environ 10 Hz comme le montre la fig.
3. Une largeur de bande de résonance aussi large est
probablement due au couplage entre les cavités de la cuvette
d'embouchure et de la bouche du joueur. Ce couplage peut se produire
parce que la résistance et l'inductance de l'ouverture de
lèvre sont négligeables dans l'excitation du premier mode
à fréquence basse5,24. Voir la section III B pour des discussions plus détaillées.
D.
Trompette et cor
La figure 7 montre les résultats expérimentaux d'une
trompette (modèle d'étude Yamaha 2320E avec embouchure
Bach 5C) et d'un cor (Alexander 103 avec une embouchure Lawson S660).
La trompette a été jouée par l'auteur qui n'avait
aucune expérience de cet instrument avant cette séance,
pendant laquelle il a essayé plusieurs embouchures
différentes. Il n'a pas pu jouer une note plus haute que la
cinquième résonance. En outre, il lui était
difficile de contrôler le volume, aussi les données
repérées par le symbole ♦ dans la fig. 7
correspondent à une émission voisine de mf.
En revanche, le cor a été joué par un musicien
semi-professionnel ayant plus de dix ans d'expérience dans des
orchestres symphoniques. Aucune consigne particulière sur la
manière de jouer ne lui a été donnée pour
l'expérience, aussi il a joué de son instrument
naturellement après quelques minutes pour s'habituer à
une lèvre supérieure équipée d'une jauge de
contrainte. Pendant l'expérience, on lui a donné des
consignes de volume sonore. Les données repérées
par le symbole o indiquent un volume au-dessous du mp;
celles repérées par le symbole • un volume au-dessus du mf.
D'après la fig. 7, la différence de phase Lp – Lξ
entre la pression dans l'embouchure et le déplacement de la
lèvre devient positive excepté pour la deuxième
résonance. En outre, excepté la 11ème
résonance du cor, cette différence de phase augmente
quand on excite les résonances supérieures. Le volume
sonore affecte la différence de phase pour le cor. Bien que des
sons plus forts de la même résonance semblent donner de
plus grandes valeurs absolues de la différence de phase, les 5ème et 11ème
résonances vont à l'encontre cette tendance. Des
résultats de la fig. 7, nous pouvons qualitativement conclure ce
qui suit : le modèle de lèvre vibrant vers
l'extérieur est applicable à la deuxième
résonance inférieure ; le modèle vertical
prédomine dans les résonances supérieures.
III. DISCUSSION
A. Formes d'onde de pression dans l'embouchure et de contrainte de lèvre
 Figure 7. Différence de phase mesurée entre la pression acoustique dans l'embouchure p et la contrainte de la lèvre du joueur ε dans la trompette et le cor. La jauge B2 a été utilisée pour la détection de contrainte. |
L'amplitude absolue de la pression dans l'embouchure est déterminée à partir de la référence 50mV interne de l'amplificateur (type 2609 de B&K) et de la sensibilité nominale (3.16mV/Pa) du microphone de mesure. Celle de la contrainte de la lèvre est déterminée par une référence interne qui peut être établie arbitrairement. Comme les signaux de pression et de contrainte sont échantillonnés toutes les 1 ms, les formes d'onde dans la fig. 8 ne sont pas aussi lisses que celles qu'on obtient avec un oscilloscope analogique. Néanmoins, la fig. 8 montre les caractéristiques communes aux cuivres : la pression dans l'embouchure pour les notes graves est pratiquement non-sinusoïdale, alors que celle des notes aiguës est presque sinusoïdale5,24. Par ailleurs, il n'y a aucun résultat expérimental antérieur avec lequel comparer la forme d'onde de contrainte. D'après la fig. 8, la forme d'onde de contrainte passe de non-sinusoïdale pour les notes graves à presque sinusoïdale pour les notes aiguës, exactement comme la forme d'onde de pression. Cependant, la forme d'onde de contrainte ne suit pas la forme d'onde de pression, en particulier pour les notes graves.
En outre, contrairement à la vibration quasi sinusoïdale de la lèvre4, la contrainte de la lèvre est non sinusoïdale. Ce caractère non sinusoïdal pourrait dépendre de l'intervalle de temps pendant lequel les lèvres se ferment. Par exemple, la forme d'onde de contrainte pour Ut3 semble montrer la fermeture de lèvres sur environ un tiers du cycle (rappelez-vous qu'une contrainte positive correspond à un déplacement négatif comme discuté dans la section I C). Cette durée de fermeture semble diminuer pour les notes aiguës et par conséquent la forme d'onde de contrainte de rapproche de la sinusoïde. Il faut cependant plus de données expérimentales pour construire une explication définitive de cette différence intéressante entre les formes d'onde de déplacement et de contrainte.
B. Fréquence jouée et fréquence de résonance
 Figure 8. Formes d'onde de pression d'embouchure et de contrainte de lèvre mesurées pour les notes Fa2, Sol3, Fa3, et La3 jouées mf au cor. |
Pour calculer la fréquence de résonance il faut évacuer le problème de la température qui détermine la vitesse du son moyenne dans les systèmes acoustiques mentionnés ci-dessus. Elliott et Bowsher5 ont soigneusement estimé la distribution de la température pour évaluer l'accord réel du trombone, basée sur la mesure suivante de Wogram34: la température décroît presque exponentiellement d'environ 33° à l'embouchure, à 26° à mi-chemin de l'instrument et à 24°C (température ambiante) au pavillon. Dans notre cas de géometries cylindriques simples pour la résonance, la température moyenne peut être estimée grossièrement à la moyenne arithmétique de la température à l'embouchure (ou à l'entrée du tube) (environ 33°C) et de la température ambiante (environ 21°C), c'est-à-dire 27°C. Cette température moyenne donne une vitesse du son moyenne de 347,4 m/S.35
Calculons d'abord les fréquences de résonance des tubes 1 et 3 (cf. section II A). Leurs longueurs acoustiques sont de 291,3 et 293,8 mm, respectivement, où la correction d'extrémité est donnée par 0,62 x (rayon de tube). Les lèvres du joueur, qui rentrent dans le tube, affectent à peine cette longueur acoustique parce que la section des tubes est beaucoup plus grande que l'ouverture des lèvres. Les fréquences de résonance des tubes 1 et 3 sont alors de 298,1 et 295,6 Hz, respectivement. Si on reporte cette fréquence de résonance sur la fig. 3, on voit que la vibration vers l'extérieur se produit au-dessus de la résonance et la vibration verticale au-dessous. Ce résultat sur la relation de fréquence est tout à fait conforme au résultat sur la relation de phase de la fig. 3, et montre la fiabilité de notre méthode de mesure de différence de phase.
Ensuite considérons les effets de l'embouchure sur la résonance. La figure 9(a) montre un circuit électrique équivalent à un instrument de la famille des cuivres se composant d'un joueur, d'une embouchure, et d'un tube résonant. Une pression constante P0 aux poumons du joueur est appliquée à l'embouchure par la trachée, la bouche et l'ouverture de lèvres du joueur. Pour les résonances basses le schéma 9(a) peut être simplifié en 9(b) parce que la résistance instantanée Rs(t) et l'inductance Ls(t) de l'ouverture de lèvre sont négligeables comparées à l'amplitude de l'impédance Zh de l'instrument5,24. En conséquence, la capacité CM de la cuvette d'embouchure est couplée avec la capacité Cm de la bouche du joueur. Comme il n'est pas facile d'estimer la force de ce couplage, le côté du joueur représenté par la capacité C0 des poumons, l'inductance de la trachée L0 et la capacité de la bouche Cm dans 9(a) sont simplifiés comme une capacité équivalente C'm dans 9(b).
Le circuit de 9(b) est applicable au calcul de la fréquence de résonance du tube Rl avec une embouchure (cf. section II C). On ne connaît pas l'expression mathématique de Zh pour les cuivres réels, mais celle d'un tube cylindrique est donnée par
Zh = jZ0 tan kl, (4)
où Z0 est l'impédance caractéristique, k le nombre d'onde et l la longueur acoustique. Pour simplifier, la dissipation d'énergie dans le tube est négligée dans l'éq. (4). La fréquence de résonance du circuit de 9(b) est donnée par le maximum de l'impédance d'entrée Zm vue de la bouche du joueur comme suit :
1/Zin = 1/(Zh + jωLM) + jωC = 0, (5)
où
(la capacité couplée) C = CM + C'm = V / ρc² (6)
(l'inductance de la queue) LM = ρlM /SM (7)
 Figure
9. Circuit électrique équivalent : (a) circuit
équivalent aux cuivres, (b) circuit simplifié pour les
cuivres dans le registre grave et pour les systèmes embouchure
– tube résonants, où on postule le couplage entre
la cuvette d'embouchure et la bouche du joueur. Figure
9. Circuit électrique équivalent : (a) circuit
équivalent aux cuivres, (b) circuit simplifié pour les
cuivres dans le registre grave et pour les systèmes embouchure
– tube résonants, où on postule le couplage entre
la cuvette d'embouchure et la bouche du joueur.
|
tan kl = (lS / V)(1 / kl) – (lM / l)(S / SM) kl (8)
en utilisant les éqs. (4), (6) et (7). Le tableau I donne les dimensions des systèmes embouchure – tube résonant R1 pour le cor et la trompette. La figure 10 montre les fréquences de résonance fres (= ck /2π) calculées à partir de l'éq. (8) et du tableau I.
Dans la fig. 10 fres est donnée en fonction du volume V de cavités couplées. Le volume de la cuvette de l'embouchure est diminué d'une quantité égale au volume déplacé par les lèvres du joueur appuyées contre le bord. Pour une embouchure de trombone, par exemple, le volume déplacé a été estimé à 2,5 ± 0,5 cm3 pour un volume de cuvette de 4,7 cm3. 22 Ce volume déplacé est estimé grossièrement à 1,5 cm3 pour le cor et à 0,5 cm3 pour la trompette (voir les courbes pleines dans la fig. 10). Le volume de cuvette est alors réduit à 1,4 cm3 pour le cor, et à 1,0 cm3 pour la trompette. Le volume de cuvette peut être encore plus réduit par les lèvres dans les conditions de jeu réelles de l'instrument. On fait l'hypothèse que le volume de cavité minimal est de 1,0 cm3 pour le cor et 0,5 cm3 pour la trompette (voir la courbe en trait plein dans la fig. 10). Une forte pénétration des lèvres dans l'embouchure, qui a comme conséquence une plus grande ouverture de lèvre, est probablement un facteur important de couplage de la cavité de la bouche du joueur avec celle de la cuvette. En faisant l'hypothèse que le volume de cavité maximal est de 3,0 cm3 pour le cor et la trompette dans les conditions de jeu, nous obtenons pratiquement la même bande de fréquences de résonance que sur la figure 6.
TABLEAU I. Dimensions des systèmes embouchure – tube résonant
|
Cor
embouchure – tube résonant R1 |
Trompette
embouchure – tube résonant R1 |
||
| Longueur acoustique du tube | l (mm) |
346
|
370
|
| Rayon du tube | a (mm) |
3.5
|
3.5
|
| Longueur de la queue d'embouchure | lM (mm) |
40
|
74
|
| Rayon de la queue d'embouchure | aM (mm) |
3.1
|
4.2
|
| Volume de la cuvette d'embouchure | VM (cm3) |
2.9
|
1.5
|
 Figure 10. Fréquence de résonance fres des systèmes embouchure – tube résonant en fonction du volume V de cavité dû au couplage entre la cuvette d'embouchure et la bouche du joueur. •: Embouchure de cor et tube résonant Rll. ♦: Embouchure de trompette et tube résonant Rl . La courbe en trait plein indique les valeurs possibles du volume de cavité dans des conditions de jeu . |
C. Vibration vers l'extérieur contre vibration verticale
Les principales questions qui se posent au vu de la fig 7 sur la différence de phase Lp – Lξ dans le cor et la trompette sont les suivantes :
(1) comment se produit la transition depuis l'oscillation vers l'extérieur dans les résonances basses vers l'oscillation verticale autour de la troisième résonance ?
(2) qu'est-ce qui produit les valeurs beaucoup plus grandes de Lp – Lξ dans les résonances supérieures du cor (au-dessus de la huitième) ?
La première question semble être liée au changement drastique de forme d'onde sonore quand la vibration passe de la plus basse résonance (la seconde) à des modes plus élevés. Ce changement dépend essentiellement des amplitudes relatives Rs /|Zh| et Ls /|Zh| dans la fig. 9.5,24 Pour les résonances basses, Rs et Ls sont négligeables comparées à |Zh| comme le montre la figure 9(b). Par conséquent, l'oscillation et la forme d'onde sont déterminées par l'impédance Zin d'entrée définies par l'éq. (5). Cette impédance Zin devrait être capacitive pour la deuxième résonance du cor et de la trompette comme on le déduit des résultats montrés à la fig. 10 sur les premières résonances des systèmes embouchure – tubes résonants parce que leur différence de phase Lp – Lξ est négative comme le montre la fig. 6. L'oscillation vers l'extérieur résulte de l'impédance capacitive d'entrée. Cette capacité de Zin peut être contrôlée par le C de la cavité couplée bouche – embouchure .
Cependant, un tel couplage direct de cavité est rompu comme indiqué fig. 9(a) quand la résistance Rs et l'inductance Ls de l'ouverture des lèvres deviennent dominantes dans les résonances supérieures. En conséquence, l'impédance Zin d'entrée vue de la bouche du joueur tend à être inductive en raison de la faible influence de l'impédance de l'instrument Zh [à vérifier toutefois par le calcul numérique du circuit présenté en 9(a) en fonction de la fréquence]. Cette situation est susceptible de provoquer la vibration verticale et des formes d'onde plus sinusoïdales qui dépendent principalement de l'impédance non-linéaire de l'ouverture étroite des lèvres. Par conséquent la transition entre les régimes vibratoires, qui correspond très étroitement à la transition entre les formes d'onde de tonalité, sera déterminée par le découplage bouche – embouchure dû à l'impédance de l'ouverture étroite des lèvres.
En outre, une ouverture étroite de lèvre produit l'effet de Bernoulli. Bien que cet effet dépende du mode de séparation des flux à l'ouverture de lèvre et que les caractéristiques de cet écoulement ne soient pas connues exactement, nous pouvons postuler son existence comme dans le cas de la vibration des cordes vocales9,10,25,26. La pression instantanée ps(t) résultant d'une réduction de pression à une ouverture étroite est donnée par :
ps(t) = –ρUv(t) (9)
dans une approximation linéaire, où U et v(t) sont la vitesse moyenne d'écoulement et la vitesse d'écoulement instantanée, respectivement. En dérivant l'éq. (9) nous avons supposé que la pression à l'ouverture Ps peut être approximée par P0 – (1/2)ρ(U + v)2, où P0 est la pression de souffle constante9. Par conséquent l'amplitude de ps(t), qui donne le mouvement ascendant, augmente généralement avec la pression du souffle. D'autre part, puisque la pression d'embouchure diminue généralement pour les modes croissants20, la vibration verticale tend à être dominante pour les résonances supérieures dans les cuivres.
Il convient de noter que la pression instantanée ps(t) de l'éq. (9) agit sur une partie A de la lèvre parallèle au sens d'écoulement, alors que la pression dans l'embouchure agit sur la partie A¹ de la lèvre perpendiculaire au sens d'écoulement. Par conséquent le rapport A/A¹ semble être une autre cause possible du changement de mode de vibration. Ce rapport change selon la configuration de la lèvre, qui dépend de la pression du souffle et de la position de l'embouchure. Des pressions de souffle élevées peuvent rendre le rapport plus grand que 1 malgré l'amincissement de la lèvre dû à la tension élastique croissante nécessaire pour augmenter sa fréquence de résonance. Cette tendance est constatée dans l'euphonium6. En utilisant les valeurs observées de la largeur efficace b et de l'épaisseur efficace de la lèvre d, et en utilisant la valeur efficace de la hauteur h de lèvre (estimée en supposant leur théorie valable36), Saneyoshi et autres6 ont évalué A (=bd /2) et A¹ (= bh). Selon le tableau IV de la réf. 6, A¹ est légèrement plus grand que A pour la note la plus basse Sibl, mais A est plus grand que A¹ pour les autres notes plus élevées. Nous pouvons déduire du résultat de la fig. 7 qu'une situation semblable s'applique probablement au cor et à la trompette.
En outre, ils ont prédit la différence de phase Lp – Lξ à partir de la fréquence de jeu mesurée et son écart par rapport à la fréquence nominale de la résonance de l'instrument [cf. l'éq. (44) et la fig. 6 de la réf. 6]. Selon leurs résultats, la différence de phase dans l'euphonium est relativement grande et des augmente de 15° environ à 50° quand la note jouée monte de la première résonance (Sib1) à la huitième (Sib4).
Cette prédiction semble rejoindre qualitativement ce qu'on a vu à la fig. 7, bien que la deuxième résonance, la plus basse, du cor et de la trompette entretienne une vibration vers l'extérieur. Cet accord suggère la vérification expérimentale de leur théorie. Dans le cas de la résonance la plus basse des tubes excités sans embouchure, les lèvres du joueur peuvent utiliser pleinement leur flexibilité pour changer le rapport A/A¹ dans une large mesure. Dans ce cas deux régimes d'oscillation peuvent apparaître dans ce système malgré de basses pressions de souffle. Mais la flexibilité des lèvres est entravée par le bord de l'embouchure. Par conséquent seule la vibration vers l'extérieur est susceptible d'apparaître dans des tubes non résonant et résonants avec une embouchure quand la note correspondant à la résonance la plus basse est jouée avec de basses pressions de souffle.
Jusqu'ici nous avons considéré les trois candidats suivants pour le changement de mode de vibration dans le cor et la trompette : (1) le découplage de la bouche et de l'embouchure, (2) l'effet de Bernoulli à un faible écartement des lèvres, et (3) le rapport A/A¹ dans la configuration de lèvre vibrante. A partir de ces trois causes possibles du changement de mode vibratoire, il faudrait étudier la mécanique des tissus musculaires pour expliquer de façon cohérente comment l'augmentation de tension musculaire nécessaire pour augmenter la fréquence de résonance des lèvres entraîne une ouverture plus étroite de lèvre (= bξ) et une plus grande valeur de A/A¹ (= d/2h) simultanément. D'autres investigations sont nécessaires pour construire une description plus définie et plus quantitative sur la transition d'oscillation et pour indiquer la cause réelle de la transition.
Il reste toujours la question mentionnée dans le point (2) du premier paragraphe de cette sous-section. Il semble que les valeurs de Lp – Lξ au-dessus de la huitième résonance du cor soient trop grandes pour entretenir l'auto-oscillation, si nous supposons qu'il n'y a pas de différence de phase entre le déplacement de la lèvre et la vitesse acoustique du volume d'air qui excite l'instrument. Supposons donc que la vitesse instantanée du flux d'air à la sortie des lèvres v(t) soit proportionnelle à la vitesse de la lèvre supérieure quand elle se ferme, comme dans la vibration des cordes vocales:9 v = –α (dξ / dt), où α désigne une constante positive. Par conséquent nous tirons de l'éq. 9 :
ps = αρU (jωξ). (10)
Comme la pression acoustique dans l'embouchure p est approchée par ps,5,6 l'éq. (10) implique qu'il y aura une différence de phase de 90° entre p et ξ si les lèvres du joueur de cuivre vibrent exactement comme le prévoit le modèle à une masse des cordes vocales.
Il est donc très possible que la vibration verticale existe aux résonances supérieures à la huitième dans le cor. Cette hypothèse est principalement dérivée de l'inductance et de la résistance de l'air à l'ouverture de lèvre, mais les détails de la différence de phase sont affectés par la pression acoustique dans la bouche du joueur5, l'écoulement autour des lèvres37, les caractéristiques de résonance de l'instrument, le niveau sonore, etc. En outre, l'auteur s'est cantonné aux modèles unidimensionnels (vibration des lèvres vers l'extérieur ou verticale) pour se concentrer sur leurs aspects fondamentaux. On obtiendrait une explication plus complète de l'auto-oscillation des lèvres du joueur de cuivre en prenant en compte des modèles bidimensionnels de lèvre plus paramétrables15,16,19 ou des modèles de cordes vocales à deux masses25,26 Néanmoins, dans le cadre des discussions ci-dessus nous pouvons conclure que la vibration propre des lèvres dans des cuivres passe de la vibration vers l'extérieur à la vibration verticale quand on joue des notes de plus en plus hautes.
IV. CONCLUSIONS
Le comportement acoustique des lèvres du joueur de cuivre a
été étudié expérimentalement sur
quatre types de systèmes acoustiques : tubes excités par
les lèvres sans embouchure, tube non résonant avec une
embouchure, tubes résonants avec une embouchure, et vrais
cuivres. La question principale était de savoir si les
lèvres du joueur vibrent vers l'extérieur ou
verticalement. On a mesuré la contrainte de la lèvre
supérieure vibrante au lieu de la vitesse de déplacement
de l'air près des lèvres en raison du caractère
pratique et de la facilité de la détection de la
contrainte tout en jouant de l'instrument. La différence de
phase entre la pression dans l'embouchure et le déplacement de
la lèvre a été dérivée de la
différence de phase entre contrainte et pression et a
été étalonnée à partir de la
pression à proximité d'un diaphragme convexe vibrant sur
lequel était fixée une jauge de contrainte. Postulant que
cette différence de phase change de la même façon
que celle de l'impédance d'entrée autour des
résonances propres du système, une valeur négative
(resp. positive) de cette différence de phase suggère une
vibration vers l'extérieur (resp. verticale) des lèvres.
Les résultats expérimentaux ont montré que :
(1) les tubes larges excités par les lèvres peuvent
entretenir les deux modes vibratoires, vers l'extérieur ou
vertical, en raison de la capacité des lèvres à
adopter facilement des configurations différentes. Mais un tube
étroit ne peut entretenir que la vibration vers
l'extérieur, et difficilement.
(2) les systèmes embouchure – tube non résonant
peuvent presque entretenir la vibration vers l'extérieur sur une
grand plage de fréquences. Le "buzzing" des lèvres
correspond à ce système acoustique.
(3) les systèmes embouchure – tube résonant peuvent
entretenir totalement la vibration vers l'extérieur. Ces
systèmes ont une bande de fréquences de résonance
beaucoup plus large que les tubes excités sans embouchure.
(4) le cor utilise la vibration vers l'extérieur pour la note la
plus grave (deuxième résonance) et la vibration verticale
pour les résonances supérieures. Dans la trompette les
deuxième et quatrième résonances entretiennent
respectivement la vibration vers l'extérieur et verticale, et
les deux sont mélangées pour la troisième
résonance.
La fréquence de résonance de l'instrument a
été calculée et comparée à la
fréquence jouée pour confirmer les résultats (1)
et (3) ci-dessus. Ce résultat, qui indique que la vibration des
lèvres vers l'extérieur (resp. verticale) se produit
à une fréquence supérieure (resp.
inférieure) à la résonance du tube, a
démontré la fiabilité de la méthode de
mesure des différences de phase. D'ailleurs, l'hypothèse
du couplage des cavités embouchure / bouche du joueur dans le
grave explique de façon plausible la largeur de bande de
résonance mentionnée en (3). Cette hypothèse est
justifiée par l'importance négligeable de
l'impédance de l'ouverture des lèvres comparée
à l'impédance d'entrée du tube5,24.
On a constaté une forte corrélation entre le
régime d'oscillation et la forme d'onde dans le cor et la
trompette : la pression dans l'embouchure dans le grave, en particulier
à la deuxième résonance, est
particulièrement non-sinusoïdale et entretenue par la
vibration des lèvres vers l'extérieur ; dans l'aigu elle
est plus sinusoïdale et entretenue par la vibration verticale des
lèvres. Nous pensons que le changement de régime
vibratoire et de forme d'onde dépendent de l'importance de
l'impédance de l'ouverture des lèvres. Si cette
impédance est négligeable en comparaison de
l'impédance d'entrée de l'instrument vue de la bouche du
joueur, le couplage de cavité entre la bouche du joueur et la
cuvette d'embouchure se produira et donnera une impédance
d'entrée capacitive qui favorise la vibration vers
l'extérieur. Cette situation est très semblable au point
(3) ci-dessus.
En revanche, quand l'impédance de l'ouverture des lèvres
arrive au même ordre de grandeur que l'impédance
d'entrée en augmentant la pression de souffle, le
découplage des cavités aura comme conséquence une
impédance d'entrée inductive qui favorise la vibration
verticale. Comme la pression instantanée de Bernoulli à
l'ouverture de lèvre et la surface de lèvre recevant
cette pression augmentent avec la pression du souffle, la vibration
verticale des lèvres tend à être
prédominante pour les résonances supérieures des
cuivres. La différence de phase entre pression et
déplacement de la lèvre approche 90° quand on choisit
une résonance au-dessus de la huitième. Ce
résultat expérimental suggère que les
lèvres du joueur de cuivre vibrent exactement comme
prédit par le modèle à une masse des cordes
vocales pour de telles résonances élevées.
Le présent article clarifie des aspects fondamentaux de la
fonction des lèvres d'un joueur de cuivre. A partir de ces
résultats, remarquons qu'il est essentiel pour les joueurs de
cuivre de travailler non pas le "buzzing" mais la flexibilité
des lèvres pour améliorer la précision du choix de
résonance. Ainsi, inutile d'avoir un tube non résonant
pour la pratique du "buzzing" parce qu'un tube non résonant
entretient la vibration vers l'extérieur qui ne peut pas
produire les notes aiguës des cuivres. Pour une analyse plus
détaillée de l'émission du son dans les cuivres,
il faudra analyser plus précisément le couplage et le
découplage entre la bouche du joueur et l'embouchure via
l'ouverture de lèvre, en particulier du point de vue de la
dynamique des fluides..
REMERCIEMENTS
L'auteur remercie le professeur George R. Plitnik de
l'université d'Etat de Frostburg d'avoir suggéré
l'expérience sur un tube non résonant et de son aide pour
l'expérience sur la trompette. L'auteur exprime également
ses remerciements à Hiroyuki Ohtsuki des Laboratoires de
Recherche sur le Traitement de l'Information Humaine ATR qui a
joué le cor et au Dr. Seiji Adachi d'ATR pour son aide dans
l'expérience avec le cor et pour ses commentaires sur le
manuscrit. L'auteur est reconnaissant au Dr. James B. Cole du
Laboratoire de Recherches Navales des États-Unis (temporairement
à l'Institut de Recherche en Communication Electrique de
l'université de Tohoku, Japon) pour sa révision soigneuse
de l'expression anglaise. L'auteur remercie également le
professeur Thoru Idogawa de l'Institut de Technologie de Saitama et le
professeur Keinosuke Nagai de l'Université de Tsukuba pour leur
soutien permanent de ces expériences. En conclusion, l'auteur
voudrait exprimer sa reconnaissance aux réviseurs anonymes, qui
ont apporté chacun des commentaires appropriés et des
suggestions valables .
1H. L. F. Helmholtz, On the Sensations of Tone, translated by A. J. Ellis (Dover, New York, 1954), pp. 95-102.
2N. H. Fletcher, "Excitation mechanism in woodwind and brass instruments," Acustica 43, 63-72 (1979); 50, 159(E) (1982).
3N. H. Fletcher, R. K. Silk, and L. M.
Douglas, "Acoustic admittance of air-driven reed generators," Acustica
50, 155-159 (1982).
4D. W. Martin, "Lip vibrations in a cornet mouthpiece," J. Acoust. Soc. Am. 13, 305-309 (1942).
5S. J. Elliott and J. M. Bowsher, "Regeneration in brass wind instruments," J. Sound Vib. 83, 181-217 (1982).
6J. Saneyoshi, H. Teramura, and S.
Yoshikawa, " Feedback oscillations in reed woodwind and brasswind
instruments," Acustica 62, 194-210 (1987).
7S. Yoshikawa, " Self-oscillation of
brass instruments viewed from one-mass vocal cord vibration,"
Proceedings of the Spring Meeting of the Acoustical Society of Japan,
pp. 379-380 (1987).
8S. Yoshikawa, "On the modeling of self-oscillation in brass instruments," J. Acoust. Soc. Am. Suppl. 1 84, S161 (1988).
9I. R. Titze, "The physics of small-amplitude oscillation of the vocal folds," J. Acoust. Soc. Am. 83, 1536-1552 (1988).
10K. Ishizaka and M. Matsudaira, "
Fluid mechanical considerations of vocal cord vibration," Monograph No.
8, Speech Communications Research Laboratory, Santa Barbara, CA (1972).
11I. R. Titze and D. T. Talkin, "A
theoretical study of the effects of various laryngeal configurations on
the acoustics of phonation," J. Acoust. Soc. Am. 66, 60-74 (1979).
12M. E. Mclntyre, R. T. Schumacher,
and J. Woodhouse, "On the oscillation of musical instruments," J.
Acoust. Soc. Am. 74, 1325-1345 (1983).
13D. H. Keefe and M. Park, " Tutorial
on physical models of wind instruments: II, Time domain simulations,"
Tech. Rep. Ser. No. 9002, School of Music, University of Washington,
1990.
14D. H. Keefe, "On sound production in brass instruments," J. Acoust. Soc. Am. Suppl. 1 87, S138 (1990).
15W. J. Strong, "Computer simulation of a trumpet," J. Acoust. Soc. Am. Suppl. 1 87, S138 (1990).
16W. J. Strong and J. D. Dudley,
"Simulation of a player- trumpet system," Proceedings of the Stockholm
Musical Acoustics Conference (unpublished).
17G. A. Redhead, "Toward a model of
sound production in the trumpet for musical synthesis," Report,
Department of Electrical and Electronic Engineering," University of
Canterbury, Christchurch, New Zealand, 1993.
18S. Adachi and M. Sato (unpublished).
19S. Adachi and M. Sato, " Brass
instrument simulation using a lip vibration model with two degrees of
freedom," Tech. Rep. of the IEICE, No. EA94-25, 1994.
20J. D. Dudley and W. J. Strong, "A
computer study of the effects of har-monicity in a brass wind
instrument : Impedance curve, impulse response, and mouthpiece pressure
with a hypothetical periodic input," Appl. Acoust. 30, 117-132 (1990).
21J. Backus, " Input impedance curves for the brass instruments," J. Acoust. Soc. Am. 60, 470-480 (1976).
22S. Elliott, J. Bowsher, and P.
Watkinson, " Input and transfer response of brass wind instruments," J.
Acoust. Soc. Am. 72, 1747-1760 (1982).
23R. Causse, J. Kergomard, and X.
Lurton, " Input impedance of brass musical instruments-Comparison
between experiment and numerical models," J. Acoust. Soc. Am. 75,
241-254 (1984).
24J. Backus and T. C. Hundley, " Harmonic generation in the trumpet," J. Acoust. Soc. Am. 49, 509-519 (1971).
25K. Ishizaka and J. L. Flanagan,
"Synthesis of voiced sounds from a two-mass model of the vocal cords,"
Bell Syst. Tech. J. 51,1233-1268 (1972).
26I. R. Titze, "On the mechanics of vocal-fold vibration," J. Acoust. Soc. Am. 60, 1366-1380 (1976).
27N. H. Fletcher, "Autonomous
vibration of the simple pressure-controlled valves in gas flows," J.
Acoust. Soc. Am. 93, 2172-2180 (1993).
28S. Yoshikawa and G. R. Plitnik, "An
experimental investigation of the phase difference between lip
vibration and acoustic pressure in brass instrument mouthpieces," J.
Acoust. Soc. Am. 94, 1834(A) (1993).
29S. Yoshikawa and G. R. Plitnik, "A
preliminary investigation of brass player's lip behavior," J. Acoust.
Soc. Jpn. (E) 14, 449-451 (1993).
30P. M. Morse, Vibration and Sound (McGraw-Hill, New York, 1948), 2nd ed., pp. 312-313.
31H. W. Henderson, "An experimental study of trumpet embouchure," J. Acoust. Soc. Am. 13, 58-64 (1942).
32R. D. Weast, "A stroboscopic analysis of lip function," The Instrumentalist 23, 44-46 (1963).
33Les termes techniques comme le
modèle d'anche vibrant vers l'extérieur et le
modèle à une masse des cordes vocales ont
été abandonnées à ce stade parce qu'on
parle maintenant de modélisation des lèvres. L'anche est
remplacée par la lèvre, la corde vocale à une
masse par la vibration verticale à une masse.
34K. Wogram, "A contribution to the
measurement of the intonation of brass instruments," Ph.D. thesis,
Technische Universitat Carolo-Wilhelmina, Braunschweig, 1972.
35L. L. Beranek, "Acoustic properties of gases," A merican Institute of Physics Handbook (McGraw-Hill, New York, 1963), 2nd ed.
36Comme Fletcher27
l'a justement remarqué, le concept d'anche vibrant vers
l'intérieur semble être physiquement inapplicable aux
cuivres. Dans la réf. 6, on a considéré
hâtivement qu'une anche qui ne vibre pas vers l'extérieur
vibre vers l'intérieur parce que la pression instantanée
de Bernoulli dans le modèle des cordes vocales est
approximée par la pression acoustique dans l'embouchure.
Cependant, comme le montre la fig. 2 de la réf. 6, le
modèle physique adopté dans la réf. 6 est
essentiellement un modèle perpendiculaire semblable à
celui montré à la fig. l (c) de la réf. 27, qui
représente le mouvement des lèvres perpendiculaire
à l'écoulement de l'air. Dans ce contexte, les concepts
d'anche vibrant vers l'extérieur ou vers l'intérieur
devraient être classés dans la catégorie des
modèles parallèles, où l'anche vibre
parallèlement au sens d'écoulement .
37A. Hirschberg, R. W. A. van der
Laar, J. P. Marrou- Maurieres, A. P. J. Wijsnands, H. J. Dane, S. J.
Kruijswijk, and A. J. M. Houtsma, "A quasi-stationary model of air flow
in the reed channel of single-reed woodwind instruments," Acustica 70,
146-154 (1990).
Traduit de l'anglais par Joël Eymard pour le site web "Tout
sur la trompette" (http://la.trompette.free.fr) avec l'autorisation de
l'auteur.