Propagation du son dans un tuyau à parois souples

Les tubes des instruments à vent ne sont pas parfaitement rigides. Dans bien des cas, on les sent vibrer quand l'instrument sonne. Quelle est l'influence du couplage entre la colonne d'air et la paroi? On montre ici que le son se propage plus lentement dans un tuyau élastique que dans un tuyau rigide. De plus, il peut y avoir déperdition d'énergie à cause du rayonnement acoustique de la paroi du tuyau vibrant. Enfin, les vibrations du tube peuvent être amorties par une viscosité interne. Sous l'influence de ces deux derniers effets (rayonnement du tube et amortissement interne de la paroi), la constante de propagation du son dans le tuyau devient complexe : le tube emprunte de l'énergie à la colonne d'air, ce qui affecte la surtension de la résonance.
Le texte ci-dessous propose une modélisation globale de ces effets, avec en particulier un calcul de la constante de propagation du son dans un tube à parois souples.

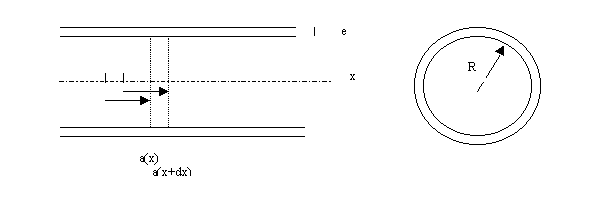
(1),

où p = P - P₀ est la surpression dans le tube, la densité de l'air, et l'élongation du mouvement de la tranche.

(2).

L'équation de la dynamique appliquée à un élément de la paroi du tube s'écrit :

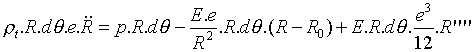(3)

Le premier terme du membre de droite est l'effort appliqué sur le tube par la colonne d'air;
Le second terme est dû à l'élasticité radiale du tube (E est le module d'Young de la paroi);
Le troisième terme est dû à la rigidité transverse du tube (effort tranchant). On peut se convaincre aisément que ce terme est négligeable devant le précédent dans tous les cas pratiques, car la longueur d'onde des oscillations transverses du tube est toujours grande devant l'épaisseur e de la paroi.

Le système d'équations différentielles (1), (2), (3) devient, en éliminant p et en posant r = R - R₀:

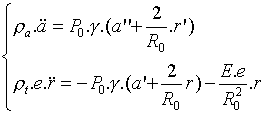(4)

On vérifie aisément que, dans l'approximation du tube rigide , on récupère l'équation habituelle pour la propagation du son en milieu libre :

.

Dans le cas général, les équations (4) couplent les oscillations de la colonne d'air et celles du tube.

Résolution du système (4) : calcul de la constante de propagation du son dans le tuyau

En prenant pour et une expression de la forme , on tire une expression pour la constante de propagation :

,

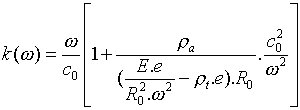où 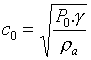est la vitesse du son en milieu infini.
Le deuxième terme de la somme entre crochets représente la correction à la relation de dispersion due à la prise en compte de l'élasticité du tube.
Cette correction peut s'exprimer en relatif :

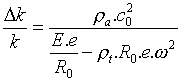   (5).

L'expression (5) est également la correction à la vitesse de propagation du son dans le tuyau; C'est aussi la correction à la fréquence de résonance du tuyau :

.

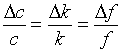Comme attendu, on trouve que cette correction tend vers zéro pour un tube très raide (grand) et très épais (grand). La correction tend également vers zéro pour un tube fait dans un matériau très dense (grand) et très épais.
Dans la plupart des cas concrets appliqués aux instrument à vent, on peut vérifier que le premier terme du dénominateur de l'équation (5) domine largement le deuxième terme, ce qui signifie qu'en utilisant un matériau de paroi plus dense, on augmentera le couplage air-tube, et on ralentira la vitesse du son dans le tuyau (ce résultat n'était pas très intuitif !).

La résonance de la paroi du tube est atteinte quand le dénominateur de l'équation (5) s'annule, c'est à dire quand

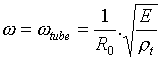(6).

En pratique, cette pulsation de résonance de la paroi est beaucoup plus haut que celle de la colonne d'air (sauf dans les tuyaux à parois très molles, cf justification dans l'application numérique ci-dessous). Quand on s'approche de ce domaine de fréquences, la constante de propagation diverge : toute l'énergie de la colonne d'air est vampirisée par le tube, le son ne se propage plus dans le tuyau !
La pulsation étant une véritable pulsation de coupure, les considérations précédentes montrent qu'il est impossible d'avoir un son riche en harmoniques avec un tuyau à parois molles, surtout si ledit tube est de grand diamètre. Ceci est vrai quelle que soit l'épaisseur de la paroi, puisque la fréquence de résonance de la paroi ne dépend pas de .

Résolution du système (4) : calcul de l'amplitude de vibration de la paroi

La résolution du système (4) permet également de déterminer l'amplitude de vibration de la paroi, ou, plus précisément, le rapport entre le mouvement de la paroi et le mouvement de l'air dans le tube :

.

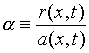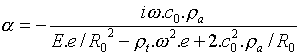Le couplage air-tube est ici purement réactif, le mouvement de la paroi est en quadrature avec celui de la tranche d'air. Si on suppose qu'on a un tube assez raide pour que la vibration de la paroi soit petite, l'abominable équation ci-dessus se simplifie :

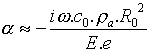(7).

Calcul de la puissance rayonnée par la paroi

Nous avons négligé jusqu'ici toutes les causes de dissipation d'énergie, en particulier l'amortissement induit par le rayonnement de la paroi vibrante. Nous l'évaluons ci-dessous en admettant que la puissance rayonnée par une tranche de tube de longueur R égale celle rayonnée par une sphère de même rayon :

,

soit, pour un tube cylindrique de longueur L, siège d'une onde stationnaire :

.

L'énergie acoustique stockée dans le tuyau vaut :

,

et la surtension associée au rayonnement par les parois vaut donc :

.

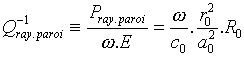En reportant la valeur pour obtenue en (6) dans le cas d'un tube assez raide, on trouve pour la surtension de rayonnement de la paroi :

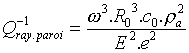. (8)

Calcul de la dissipation par amortissement interne de la paroi

Nous considérons ici une deuxième cause de dissipation d'énergie dans le couplage air-tube : l'amortissement interne du matériau du tube. La surtension associée vaut :

,

où est l'énergie stockée dans la paroi, est l'énergie acoustique totale stockée dans la paroi et dans la colonne d'air, et où est l'angle de pertes du matériau du tube.

Dans l'approximation du tube raide, le rapport vaut , donc d'après (7) :

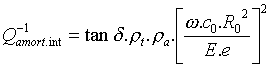(9).

Dans le domaine de fréquences acoustiques qui nous intéressent ici, l'angle de perte du bois ou des polymères est de l'ordre de 0.05, et celui des métaux est nettement plus petit encore. Dans l'approximation du tube raide, le rapport est toujours inférieur à 10^-6. Compte-tenu de ces valeurs, la dissipation par amortissement interne de la paroi est négligeable devant les autres causes de dissipation dans tous les cas pratiques. Encore fallait-il le vérifier !

Application numérique à des cas concrets :

= 1.3 Kg.m-3

= 330 m.s-1

= 10¹¹ Pa (tube métallique)

= 5.10^-4 m (épaisseur de paroi standard)

= 6. 10^-3 m (rayon du tube dans la partie étroite et cylindrique de la perce)

= 8.10³ kg.m-3 (densité du cuivre ou du laiton)

= 5. 10³ rd.s-1 (pulsation correspondant à peu près au milieu de la tessiture)

Avec ces valeurs numériques, l'écart de l'expression (5) donne 1.7 10^-5 . On constate que l'effet est petit (0.03 cents). Même si la paroi de l'instrument vibre, ça n'affecte guère les résonances de l'instrument !
Le rapport (eq.7) est ici de l'ordre de 10^-6, la paroi vibre donc très peu.
La pulsation de résonance du tube donnée par l'expression (6) vaut dans le cas de la trompette : 5. 10⁵ rd/s (environ 100 kHz) : on est dans le domaine des ultrasons, ce qui explique que le couplage tube-colonne d'air soit faible. D'après l'équation (8), la surtension de rayonnement de paroi vaut = 3.10^-9, valeur tout à fait négligeable.
Le calcul ci-dessus a été fait pour un tuyau cylindrique. Il faut s'attendre à un couplage air-tube plus fort que celui évalué ici dans la partie conique de la perce (pavillon), partie dans laquelle la paroi du tube s'amincit jusqu'à 0.3mm, avec un rayon qui augmente beaucoup.
Pour un tube de 6 cm de diamètre et 0,3 mm d'épaisseur (valeurs moyennes d'un pavillon de trompette), et au niveau d'un contre-ut (fréquence d'environ 1000 Hz), la variation relative de fréquence atteint 0,24 millièmes, soit presque un demi cent.
D'après le modèle ci-dessus, on doit pouvoir diminuer l'épaisseur du métal du tube d'une trompette jusqu'à 0.2 mm sans trop de problèmes de justesse. En revanche, la pulsation de résonance du tube au niveau du pavillon rentre dans les fréquences audibles : dans ce dernier cas, elle est de l'ordre de 10 Khz. Il pourrait se faire que la coupure des fréquences supérieures (prédite par le modèle) affecte le timbre de l'instrument. De façon assez contre-intuitive, c'est l'instrument à pavillon épais qui devrait avoir le moins de pertes, et donc le timbre le plus riche ! Qu'en disent les facteurs ?

Les formules ci-dessus sont vérifiables, mais je n'ai pas encore essayé : on peut envisager le protocole expérimental suivant : prendre deux tuyaux longs de 2 m environ, et de même diamètre interne, 1.2 cm. L'un métallique et à parois épaisses, servira de référence. L'autre en caoutchouc, servira de test.
On met sur ces deux tuyaux une embouchure de trompette (ou de clarinette, c'est mieux, le champ de liberté en fréquence est plus réduit), et on mesure la fréquence de résonance des premiers partiels à l'accordeur électronique. Le module d'Young du plastique de tuyau d'arrosage est de l'ordre de 10⁸ Pa; On attend un d'environ 30 cents, qui doit être observable. La surtension du système est également mesurable par analyse du transitoire d'extinction avec un logiciel de transformée de Fourier rapide.

La différence principale avec le cas précédent vient du module d'Young du tube, estimé deux ou trois ordres de grandeur plus faible que pour un métal : E = 10⁸ à 10⁹ GPa. Cette différence est partiellement compensée par l'épaisseur accrue du tube : 5 mm contre 0.5 pour un tube métallique.
La conclusion n'est pas la même que pour la trompette : certes, est de l'ordre de 1 cent, valeur pratiquement négligeable. Mais la pulsation de résonance du tube n'est plus nécessairement très élevée, et peut se trouver dans le domaine audible, affectant le timbre de l'instrument si le matériau de paroi est particulièrement mou. D'autre part, la surtension de rayonnement paroi n'est plus négligeable dans l'aigu de la flûte : d'après l'équation (8), est de l'ordre de 10^-2, valeur proche du seuil d'autoentretien. On commencerait à avoir des difficultés de facture instrumentale avec des tubes de plastique ou de bois très minces, ou pire encore, des tubes de carton...Mes essais de fabrication de flûtes dans des tubes PVC électriques à parois minces ont toujours été assez décevants. D'après le calcul ci-dessus, ce mauvais résultat pourrait être imputable à une déperdition d'énergie par rayonnement des parois. Là encore, l'analyse du transitoire d'extinction du son par transformée de Fourier rapide doit permettre d'apporter une confirmation expérimentale à ces élucubrations.

 
 

© Juin 2002