par BB Ninob
20 Septembre 2002
![]() Ocarinas
Ocarinas
par BB Ninob
20 Septembre 2002
Pourquoi s'y intéresser?
Un instrument pédagogique
Comment c'est fait?
Morphologie d'un ocarina
Comment ça marche?
Fréquence propre d'un ocarina. Corrections de longueur.
Spectre d'un ocarina
Familles d'ocarinas. Masse et raideur effectives d'un ocarina
Notion de famille d'ocarinas de même fréquence, mais de masse et
de raideur différentes.
Couplage au jet : pourquoi le son monte quand on souffle
plus fort
Amortissement du mode Helmholtz.
1) Puissance rayonnée
2) Puissance perdue par non adiabaticité dans le gaz
3) Puissance perdue par transferts de chaleur aux parois.
4) Puissance perdue par perte de charge dans les ouvertures
5) Puissance perdue par mise en vibration des parois du résonateur.
Surtension d'un ocarina
Le seuil d'autoentretien se traduit-il par une valeur limite
du coefficient d'amortissement?
Les ocarinas trop amortis refusent de sonner
Fabrication des ocarinas
Un procédé de fabrication simple, à la portée des
bricoleurs maladroits
Quelques règles sur les proportions des ocarinas
Plans complets de quelques ocarinas, avec leur table de doigtés
Pour accorder un ocarina
Utiliser un ocarina pour contrôler la fréquence de l'effet Larsen.
Peut-on faire de la musique comme ça?
Pourrait-on fabriquer des ocarinas à anche solide?
Un programme pour calculer la justesse des ocarinas
Pourquoi s'y intéresser?
Les ocarinas sont faciles à fabriquer, et ont un joli son très
doux. Ce sont des instruments d'apprentissage facile, sur lesquels il est quasiment
impossible de faire des "canards" (on verra plus loin pourquoi). En contrepartie,
ce sont des instrument pauvres (l'étendue est seulement d’une
octave), mais qui se prêtent bien au jeu d'ensemble. Ils peuvent faire
une bonne introduction à la flûte à bec car les doigtés
sont potentiellement identiques. Les professeurs de musique des collèges
se casseraient moins les oreilles s'ils faisaient apprendre l'ocarina à
leurs élèves (avec des instruments qui pourraient être fabriqués
par les élèves eux-mêmes en classe de technologie, sous
l'œil bienveillant du professeur de physique : joli projet pédagogique!).
Du point de vue de l’acoustique, les ocarinas sont des systèmes
simples pour faire des expériences intéressantes sur le mécanisme
d’auto-entretien du son, et le couplage entre le jet d’air et le
résonateur.
Le texte ci-dessous abordera les deux aspects : physique et fabrication. L'idée
est de bien comprendre comment ça marche, pour pouvoir faire de bons
ocarinas.
Comment c'est fait?

Conceptuellement, un ocarina est simplement une bouteille avec un goulot. Le
son est produit en soufflant sur le bord du goulot.
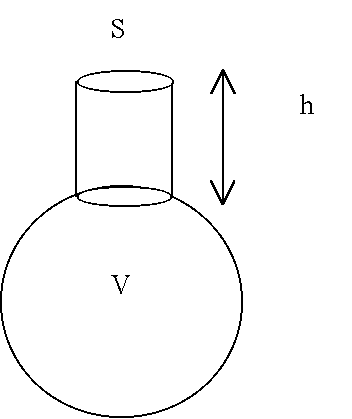
Dans la pratique, l'embouchure a une géométrie un peu plus compliquée,
avec un porte-vent, sorte de canal destiné à guider l'air vers
le bord du goulot à travers une ouverture rectangulaire (la lucarne d'embouchure).
Le bord opposé de l'ouverture est aiguisé en forme de biseau,
comme sur une flûte à bec :
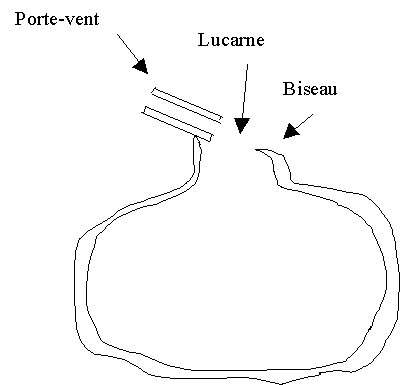
Un ocarina vu en coupe
Outre le trou d’embouchure, sur les véritables ocarinas, la bouteille est percée en général de plusieurs trous bouchés par les doigts. En les débouchant successivement, on modifie la hauteur du son produit, avec des doigtés qui peuvent être analogues à ceux d'une flûte.
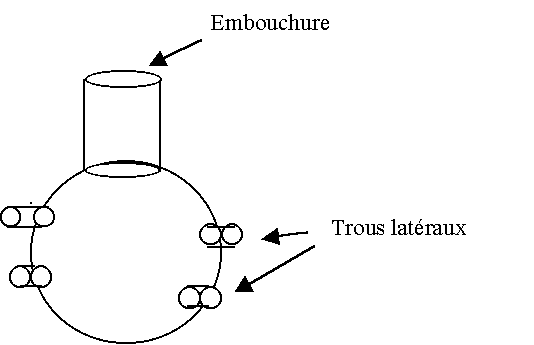
Comment ça marche?
L’ocarina est en fait un résonateur de Helmholtz, muni d'une embouchure
de flûte. L’air contenu dans la bouteille joue le rôle d’un
ressort qui fait osciller la masse d’air contenue dans les cheminées.
L’auto entretien du son se fait comme dans une flûte, grâce
à l'instabilité du jet d'air qui vient se briser sur le biseau
de l'embouchure. A la différence d’une flûte, la position
des trous est indifférente, et n’influe pas sur la hauteur du son.
La forme de la bouteille n'a pas non plus d'influence sur le système,
pourvu que son goulot soit court, et son ventre bien rebondi. En revanche, une
bouteille très allongée se comporterait comme une flûte
ou un bourdon.
Le mode Helmholtz (H) est en général beaucoup plus bas en fréquence
que les modes propagatifs (P), pour lesquels l’oscillation de l’air
prend la forme d’une onde de compression qui se réfléchit
sur les parois du récipient. Cependant, si on souffle très fort
dans un ocarina, on peut arriver à exciter ces modes propagatifs ;
mais l’obliger à se comporter comme une flûte amène
l’ocarina à devenir quelque peu criard !
Sans aller jusqu’à ces extrêmes, on constate expérimentalement
que souffler plus fort dans un ocarina fait monter le son, ce qui peut s’expliquer
en notant que le résonateur de Helmholtz est couplé au jet d’air,
dont la fréquence propre monte si la vitesse de l’air augmente.
Le formalisme ci-dessous fournit une description plus mathématique du
phénomène. Celle-ci est largement empruntée à Lord
Rayleigh (Sound Theory), avec quelques ajouts de mon cru.
Fréquence propre d'un ocarina
On s'intéresse ici à la fréquence propre d'un résonateur
de Helmholtz, parce qu'on veut comprendre ce qui détermine la justesse
de l'instrument.
En première approximation, on assimile la masse d’air contenue
dans le goulot de l’ocarina à un piston, et celle contenue dans
la bouteille elle-même à un ressort. Dans cette approximation,
l’ocarina est un oscillateur à un degré de liberté.
On écrit l’équation de la dynamique pour la masse d’air
contenue dans chaque trou débouché, ce qui amène à
un système d’équations avec autant d’équations
que de trous débouchés. La résolution de ce système
(très facile) donne la pulsation propre du mode H :
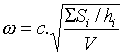 (eq.1),
(eq.1),
où c est la vitesse du son dans l'air (343 m/s pour
de l'air à 20°C et 100% d'humidité).
L’air oscille en phase dans tous les trous débouché, et
l’amplitude de l’oscillation dans le trou j est inversement proportionnelle
à la hauteur de la cheminée :
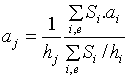
où la somme porte sur tous les trous débouchés
(i), y compris le trou d'embouchure (e).
Dans ce formalisme, l'ensemble des trous débouchés se comporte
comme un goulot unique. L’impédance de l’ocarina au niveau
de l’embouchure vaut :
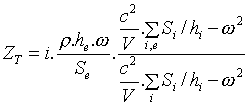 (eq. 2),
(eq. 2),
où ρ est la densité de l'air. La pulsation
propre du résonateur est celle qui annule cette impédance : ZT=0,
ce qui redonne l'éq. 1.
En deuxième approximation, on ne néglige plus les phénomènes
propagatifs dans le goulot.
Dans le goulot, la pression et l'amplitude de l'onde sonore ont la forme suivante
:
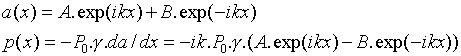 ,
,
où k est la constante de propagation du son, P0
est la pression atmosphérique (P0 = 1.e5 Pa) et γ
le rapport Cp/Cv pour l'air (γ=1.4).
Les conditions aux limites sont :
![]() = pression
acoustique dans la bouteille =
= pression
acoustique dans la bouteille = ![]() ,
,
et ![]() .
.
Les modes permis sont alors donnés par ![]() .
.
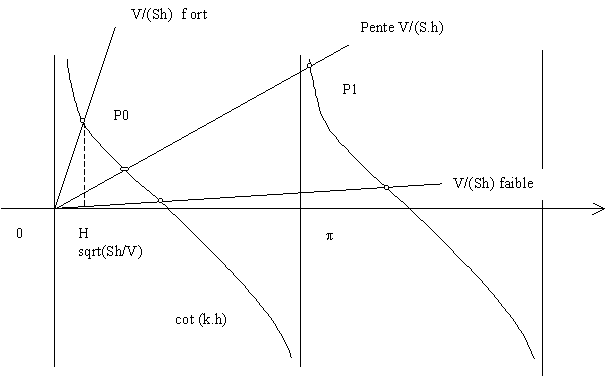
Résolution graphique de l'équation cot (kh)=V/(Sh) . (kh).
La constante de propagation k étant proportionnelle à
la pulsation ω, l'axe des abcisses donne les pulsations propres du système.
Celles-ci se trouvent aux intersections entre les courbes cot et les droites
de pente V/(Sh).
Si le rapport V/(Sh) entre le volume de la bouteille et le
volume du goulot est petit, on est ramené au cas d’un bourdon (tube
cylindrique fermé à un bout).
Si V/(Sh) est grand, cot(k.h) ~ 1/(k.h), et la pulsation du mode P0 vaut omega
= c.sqrt(S/V.h).
Le mode Helmholtz décrit plus haut s’identifie au mode P0, premier
mode propagatif. L’expression du paragraphe précédent pour
la pulsation du mode Helmholtz se retrouve ici comme une approximation, d’autant
meilleure que V/(S.h) est plus grand.
Dans tous les cas, et quel que soit le volume de la bouteille, les modes supérieurs
sont proches des infinis de la courbe cot(k.h), c’est-à dire ceux
d’une flûte cylindrique de longueur h, ouverte aux deux bouts.
Corrections de longueur pour un trou de jeu
La hauteur h d’un trou débouché n’est pas exactement
égale à la hauteur géométrique de la cheminée.
Il faut tenir compte du fait que le bouchon d’air présent dans
un trou débouché génère une onde sphérique
à l’extérieur. Le raccordement du champ de vitesses entre
l’intérieur et l’extérieur du trou ne peut être
brutal et se fait sur une longueur caractéristique du même ordre
de grandeur que le diamètre du trou. Ceci amène à introduire
une correction à la hauteur d’un trou débouché. Pour
un ocarina, j’ai déterminé empiriquement ce que valait cette
correction de longueur en faisant varier la hauteur de la cheminée latérale
d’un résonateur et en mesurant à l’accordeur électronique
comment évoluait la fréquence. Le meilleur accord avec l’expérience
est obtenu avec une correction de longueur égale à racine
carrée de la section du trou, soit 0.8 * diamètre du trou .
Correction de longueur pour le trou d'embouchure
Les choses sont un peu plus difficiles pour le trou d'embouchure, car la géométrie
de l'embouchure est plus compliquée. La forme générale
est la suivante :
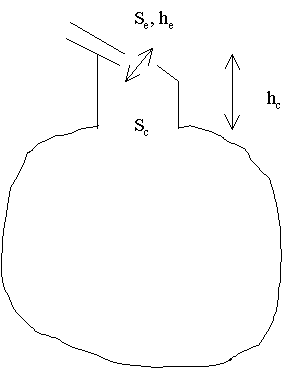
Dans le cas général, l'embouchure de l'ocarina présente
deux rétrécissements : le premier entre le ventre et le col de
la bouteille; le second entre le col et la lucarne d'embouchure. Le col est
parfois peu marqué, au point d'être inexistant.
Dans ce schéma, Sc est la surface du col et Se
est la surface de la lucarne d'embouchure; hc est la hauteur géométrique
du col et he est la hauteur effective de la lucarne d'embouchure.
Celle-ci vaut la hauteur géométrique de la lucarne (épaisseur
de la paroi dans laquelle ladite lucarne est percée), plus une correction
de longueur égale à racine de Se, comme pour un trou
de jeu :
![]() .
.
On peut montrer que cette embouchure à deux rétrécissements se ramène à un goulot équivalent, de section et de hauteur données par :
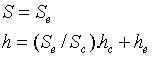 ,
,
ce qui donne une pulsation propre :
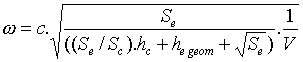 .
.
Si Se/Sc est très petit (cas d'un rétrécissement très marqué entre le col et la lucarne d'embouchure, ou cas d'un col très peu marqué), l'équation ci-dessus indique que l'ocarina se comporte comme si le véritable goulot était la lucarne d'embouchure elle même (de paramètres Se,he), plutôt que le col (de paramètres Sc, hc). On peut alors considérer celui-ci comme faisant partie intégrante de la bouteille. Si en plus la lucarne d'embouchure est percée en paroi mince, sa hauteur géométrique est faible, et la hauteur effective de la lucarne vaut racine (Se). Dans ce cas, la pulsation du résonateur vaut :
![]() .
.
Le spectre d’un ocarina
Si on considère un ocarina avec un rapport V/(Sh) élevé,
le premier mode propagatif de goulot a pour pulsation ![]() ,
comme si le goulot était ouvert aux deux bouts. En général,
ce mode a une pulsation beaucoup plus élevée que celle
du mode H, ce qui justifie ce qui a été dit plus haut sur l’isolement
du mode Helmholtz, considéré comme le seul excitable en pratique
sur un ocarina.
,
comme si le goulot était ouvert aux deux bouts. En général,
ce mode a une pulsation beaucoup plus élevée que celle
du mode H, ce qui justifie ce qui a été dit plus haut sur l’isolement
du mode Helmholtz, considéré comme le seul excitable en pratique
sur un ocarina.
Cependant, un ocarina de grande section de goulot (S grand) et de faible volume
(V petit) ne se comporte pas selon ce schéma idéal : l'approximation
de l'eq. 1 n'est plus bonne; Le rapport de fréquences entre le mode P1
et le mode P0 (ex mode H) tend vers 3/2 quand V tend vers 0. L’ocarina
se comporte alors comme un bourdon réduit à un tuyau (le goulot)
fermé à son extrémité basse.
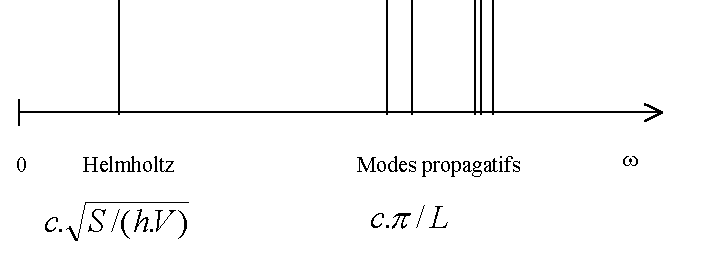
Le spectre des modes propres d'un ocarina. On a représenté
ici plusieurs modes propagatifs correspondant au mode de goulot (de pulsation
c.π/h) et à des modes de "ventre" (de pulsation
c.π/L, oω L est la taille caractéristique
de la bouteille). L'isolement du mode Helmholtz explique pourquoi un ocarina
ne fait pas de "canards", même entre les mains du musicien le plus maladroit
Familles d’ocarinas. Masse et raideur
effectives d'un ocarina
L'équation (1) donnant la fréquence d’un ocarina montre
qu’il est possible d’avoir des ocarinas de même fréquence
avec des paramètres géométriques différents :
par exemple, un ocarina de grand volume avec un goulot court sonnera à
la même fréquence qu’un ocarina de petit volume et goulot
long, pourvu que le rapport S/(hV) soit le même sur les deux instruments.
De même, deux ocarinas ayant le même volume mais des goulots de
taille différente pourront eux aussi sonner à la même fréquence,
pourvu que le rapport S/h des deux goulots reste le même.
On aboutit ainsi à la notion de famille d'ocarinas de même fréquence,
mais de géométries différentes. Bien que ces ocarinas sonnent
à la même hauteur, nous verrons plus loin qu’ils se comportent
différemment, car leur " raideur " est différente.
L’oscillation de l’air dans tous les trous débouchés
se fait en phase. L’ocarina est formellement analogue à un oscillateur
à un seul degré de liberté, c’est-à dire à
un oscillateur masse-ressort.
La masse effective et la raideur effective de l’oscillateur correspondant
valent respectivement :
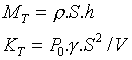
Si on a plusieurs trous débouchés, ces équations se généralisent à :
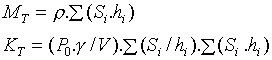
L’ocarina sera dit "raide" si K est grand (S grand, V faible), et " mou " dans le cas contraire.
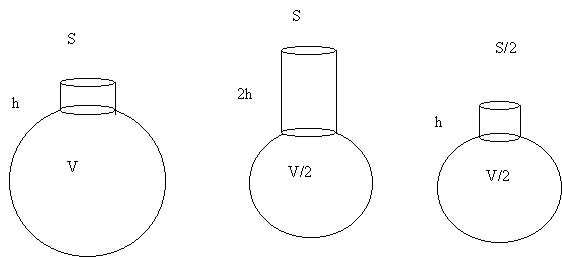
Ces trois ocarinas ont même fréquence, mais celui de gauche
est plus mou que les deux de droite.
On verra plus loin que les ocarinas mous ont un champ de liberté
en fréquence plus large que les raides.
Couplage au jet
Sur un ocarina comme sur une flûte, le son monte quand on souffle plus
fort (sans pour autant sauter au partiel supérieur comme sur une flûte
car les modes P sont très éloignés). Ce phénomène
peut s'expliquer si on admet l'existence d'un couplage entre le jet d'air (excitateur)
et le résonateur.
La façon la plus simple de formaliser ce couplage est d'écrire
que l'amplitude de vibration aA du jet d'air est proportionnelle
à l'amplitude de vibration aT de l'air dans le trou d'embouchure.
Cette prescription donne des résultats très satisfaisants pour
les flûtes, c'est pourquoi nous la conservons pour les ocarinas :
![]() ,
,
où ![]() est la constante de couplage entre le jet et l’embouchure, éventuellement
complexe si l'oscillation du jet est déphasée par rapport à
celle de l'air dans le goulot.
est la constante de couplage entre le jet et l’embouchure, éventuellement
complexe si l'oscillation du jet est déphasée par rapport à
celle de l'air dans le goulot.
L’impédance totale du système au niveau de l’anche
vaut alors, comme pour une flûte :
![]() (eq. 3),
(eq. 3),
où ![]() est l’impédance du jet seul. Celle-ci peut être évaluée
en assimilant le jet à une lame encastrée de masse effective MA
et de raideur KA :
est l’impédance du jet seul. Celle-ci peut être évaluée
en assimilant le jet à une lame encastrée de masse effective MA
et de raideur KA :
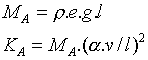
où ![]() est la vitesse du jet, et
est la vitesse du jet, et ![]() un paramètre proche de l'unité destiné à décrire
de façon effective les détails de la géométrie du
jet.
un paramètre proche de l'unité destiné à décrire
de façon effective les détails de la géométrie du
jet.
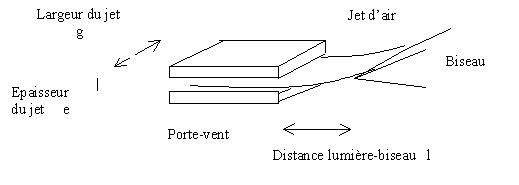
Les paramètres du jet d'air
Les paramètres MA, KA d’une
anche aérienne (jet d’air) peuvent être évalués
assez facilement : les paramètres géométriques du jet (largeur,
épaisseur, distance lumière-biseau) sont directement mesurables;
Quant à la vitesse du jet, on peut l'évaluer à partir de
quelques considérations sur la relation débit-pression au voisinage
de la bouche, et sur la capacité des poumons lors de l'expiration. Les
deux méthodes donnent des résultats concordants : la vitesse du
jet d'embouchure d'un ocarina v est de l'ordre de 5 à 25 m/s, comme sur
une flûte à bec.
L'impédance du jet seul vaut :
![]() (eq. 4),
(eq. 4),
et sa pulsation propre vaut
![]() (eq. 5).
(eq. 5).
Si on prend des valeurs numériques réalistes
pour e, g, l, v, on constate que la pulsation propre du jet est proche de celle
du résonateur, à condition de prendre ![]() ,
ceci quel que soit l'ocarina (ou même la flûte) considéré.
,
ceci quel que soit l'ocarina (ou même la flûte) considéré.
Le système couplé se comporte lui-même comme un oscillateur
à un degré de liberté, dont les paramètres sont
:
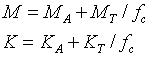
La fréquence de résonance du système couplé vaut :
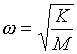 .
.
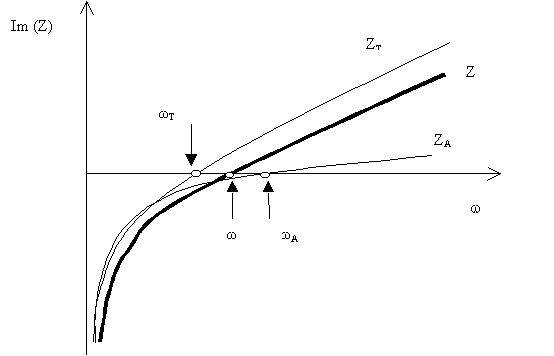
L’impédance d’un ocarina, vue du jet d’air. ZT
est l’impédance du résonateur, ZA est l’impédance
du jet d’air seul, Z est l’impédance du système couplé.
La pulsation propre du système est le zéro de la fonction impédance.
Dans l’exemple montré ici, la pulsation propre du jet est supérieure
à celle du résonateur, et la pulsation du système couplé
est située entre ces deux pulsations propres. Toute augmentation de la
vitesse du jet a pour conséquence une augmentation de la pulsation propre
du jet, et donc de la pulsation du système couplé : le son
monte.
On peut en général considérer que le couplage au jet n'apporte qu'une petite perturbation à la pulsation propre du système, parce que les paramètres MA, KA sont petits devant MT, KT. Dans ces conditions, la perturbation de la pulsation propre vaut :
![]()
Le taux de variation de la fréquence en fonction de la variation de vitesse du jet vaut :
![]()
Toutes choses égales par ailleurs, l'ocarina sera donc
"raide" si la section de son goulot S est grande et/ou si son volume V est petit.
Cette expression a été confrontée à l'expérience.
Le protocole expérimental était le suivant : on souffle dans un
ocarina de géométrie connue, en mesurant simultanément
la pression de bouche (avec un manomètre à eau), le temps d'expiration
et la fréquence du son (avec un accordeur électronique). La pression
de bouche permet d'évaluer la vitesse du jet, connaissant la géométrie
du porte-vent. Le temps d'expiration donne également la vitesse du jet,
connaissant la capacité des poumons de l'instrumentiste. Ces deux évaluations
indépendantes concordent, ce qui donne confiance dans l'évaluation
de v. Le résultat expérimental est donné ci-dessous :
Les paramètres du système étaient les suivants :
Résonateur de Helmholtz : V = 3.1 e-4 m3, S = 2.e-4 m2, h
= 5.e-2 m, ce qui donne omega = 1379 rd/s, en bon accord avec la
théorie (eq. 1).
Jet : l = 1.e-2 m, g = 2. e-2 m, e = 1.e-3 m, v = 10 à 20 m.s-1.
Expérimentalement, sur cet ocarina, le son monte d'un demi ton quand
la vitesse de l'air passe de 10 à 20 m.s-1, ce qui donne un ![]() de 5.8 e-3 s.m-1.
de 5.8 e-3 s.m-1.
Avec ces paramètres, le ![]() prédit par la théorie est de 2.2 e-3
prédit par la théorie est de 2.2 e-3 ![]() .
Si on conserve
.
Si on conserve ![]() ,
on a donc un bon accord théorie expérience avec
,
on a donc un bon accord théorie expérience avec ![]() proche
de 1 (1.3, plus exactement). On en conclut que le jet et l'air de l'embouchure
oscillent en phase, ou du moins que le déphasage (symbolisé par
une valeur complexe de la constante de couplage
proche
de 1 (1.3, plus exactement). On en conclut que le jet et l'air de l'embouchure
oscillent en phase, ou du moins que le déphasage (symbolisé par
une valeur complexe de la constante de couplage ![]() ),
est faible.
),
est faible.
Un bon indicateur de la largeur du champ de liberté en fréquence
de l’ocarina est la pente de la fonction impédance du résonateur
![]() au voisinage de
la résonance.
au voisinage de
la résonance.
Un calcul simple montre que ![]() ,
et ne dépend donc que d’un seul paramètre géométrique
de l’ocarina : la hauteur de son goulot. L’ocarina aura donc
une fréquence d’autant plus stable (champ de liberté réduit)
que la hauteur de ses cheminées sera plus grande (ocarina raide). Avec
ce nouvel indicateur, on retrouve la morphologie des ocarinas raides : un ocarina
raide possède un goulot long, nécessairement associé à
une section de goulot S large et/ou à un volume V faible pour maintenir
la fréquence constante.
,
et ne dépend donc que d’un seul paramètre géométrique
de l’ocarina : la hauteur de son goulot. L’ocarina aura donc
une fréquence d’autant plus stable (champ de liberté réduit)
que la hauteur de ses cheminées sera plus grande (ocarina raide). Avec
ce nouvel indicateur, on retrouve la morphologie des ocarinas raides : un ocarina
raide possède un goulot long, nécessairement associé à
une section de goulot S large et/ou à un volume V faible pour maintenir
la fréquence constante.
Dans le cas d’un ocarina muni de trous latéraux, le calcul est
à peine plus compliqué. La quantité ![]() est plus grande quand le nombre de trous débouchés augmente :
le couplage au jet est plus sensible sur les notes du bas que sur les notes
du haut, l'ocarina est plus raide dans le haut de sa tessiture.
est plus grande quand le nombre de trous débouchés augmente :
le couplage au jet est plus sensible sur les notes du bas que sur les notes
du haut, l'ocarina est plus raide dans le haut de sa tessiture.
On peut faire le même calcul pour un flûte : il vient ![]() ,
où L est la longueur du tube (la flûte a plusieurs modes possibles,
mais la pente dZ/domega est la même au voisinage de toutes les résonances).
,
où L est la longueur du tube (la flûte a plusieurs modes possibles,
mais la pente dZ/domega est la même au voisinage de toutes les résonances).
La longueur L d’une flûte est en général considérablement
plus grande que la hauteur h du goulot d’un ocarina de même fréquence :
on prédit donc que la largeur du champ de liberté en fréquence
d’une flûte est considérablement plus réduit que celle
d’un ocarina, ce qui est qualitativement conforme à l’expérience.
Amortissement du mode Helmholtz.
On s'intéresse ici aux phénomènes qui contribuent à
amortir l'oscillation de l'air dans le résonateur car, comme on le verra
plus loin, les phénomènes dissipatifs jouent un rôle important
sur la capacité de l'ocarina à émettre un son.
Considérons un résonateur de Helmholtz en vibration, avec une
amplitude a du déplacement de l'air au niveau du goulot. L'énergie
stockée dans le résonateur vaut :
![]() .
.
Si E est l'énergie stockée dans le résonateur, et P la puissance dépensée pour assurer le maintien de l'oscillation, on définit le "coefficient de surtension" du résonateur par :
![]() .
.
L'atténuation de l'oscillation peut être dû à différentes causes que nous examinerons successivement, en évaluant pour chacune le "coefficient d'amortissement", défini comme
![]()
1) Puissance dissipée par rayonnement à travers les ouvertures du résonateur
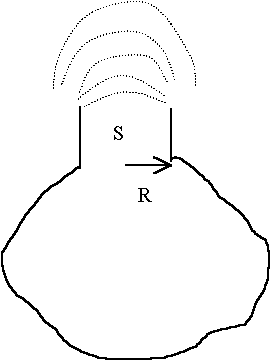
La puissance rayonnée par une demi-sphère pulsante de rayon R vaut :
![]()
Une valeur typique de la puissance rayonnée par un ocarina
est 10 mW. On en déduit que l'amplitude de l'oscillation de l'air au
niveau du goulot est de l'ordre de 2 mm.
L'amortissement de rayonnement vaut :
![]() .
.
Pour un ocarina typique, cet amortissement est de l’ordre
du pourcent. Il ne dépend pas de la taille de l’ocarina, et reste
du même ordre pour un ocarina soprano ou pour un ocarina contrebasse.
Attention cependant : on a supposé ici que seul le goulot rayonnait.
En fait, tous les trous ouverts rayonnent :
![]()
Les pertes par rayonnement augmentent donc très vite
dans l’aigu de la tessiture de l’instrument, à cause de l'exposant
sur ![]() , et à
cause du fait que beaucoup de trous sont débouchés. Cette cause
d'amortissement peut amener l’ocarina au dessous du seuil d’autoentretien
du son. Expérimentalement, on constate en effet que les ocarinas sonnent
moins facilement dans le haut de leur tessiture. Pour savoir si un instrument
est bon, testez-le dans l'aigu, tous les trous débouchés!
, et à
cause du fait que beaucoup de trous sont débouchés. Cette cause
d'amortissement peut amener l’ocarina au dessous du seuil d’autoentretien
du son. Expérimentalement, on constate en effet que les ocarinas sonnent
moins facilement dans le haut de leur tessiture. Pour savoir si un instrument
est bon, testez-le dans l'aigu, tous les trous débouchés!
2) Puissance perdue par pertes viscothermiques dans le gaz
On peut évaluer ce terme de la façon suivante :
![]()
où ![]() est
l'angle de perte
est
l'angle de perte ![]() correspondant
au rapport entre les parties réelle et imaginaire de la constante de
propagation du son dans l'air libre.
correspondant
au rapport entre les parties réelle et imaginaire de la constante de
propagation du son dans l'air libre.
Une autre expression pour ![]() est
est
![]() , où
, où ![]() est
la longueur d'onde et
est
la longueur d'onde et ![]() la distance d'atténuation du son. Cette distance est inversement proportionnelle
au carré de la fréquence, et vaut typiquement plusieurs km à
500 Hz (ref : A Physicist's Desk Reference). Par conséquent
la distance d'atténuation du son. Cette distance est inversement proportionnelle
au carré de la fréquence, et vaut typiquement plusieurs km à
500 Hz (ref : A Physicist's Desk Reference). Par conséquent ![]() est
de l'ordre de quelques e-4 aux fréquences
acoustiques usuelles. La contribution de ce type de pertes à la surtension
globale d'un ocarina est donc tout à fait négligeable.
est
de l'ordre de quelques e-4 aux fréquences
acoustiques usuelles. La contribution de ce type de pertes à la surtension
globale d'un ocarina est donc tout à fait négligeable.
3) Puissance perdue par transfert de chaleur aux parois.
Il faut également tenir compte des pertes viscothermiques liées
au transfert de chaleur à la paroi du résonateur. Cette cause
de dissipation se met également sous forme d'un angle de pertes
![]()
où k est cette fois la constante de propagation du son dans le résonateur (et non plus dans l'air libre). Pour un tuyau de périmètre Peri et de section S, la formule de Kirchoff donne :
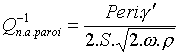
où ![]() est
une constante égale à 6.5 e-3
USI.
est
une constante égale à 6.5 e-3
USI.
Appliquée à un ocarina de surface interne Sint et de
volume V, cette équation devient :
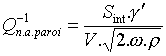
On notera que cette équation n'est pas invariante d'échelle,
et que l'amortissement viscothermique par transfert de chaleur aux parois est
moins important pour les grands ocarinas que pour les petits.
L'application numérique donne, pour des ocarinas à paroi lisse,
![]() =1% (oca soprano)
et 5.e-4 (oca basse). L'amortissement associé
est donc plutôt faible par rapport aux autres causes, mais peut devenir
significatif pour des instruments à parois rugueuses (Sint
grand).
=1% (oca soprano)
et 5.e-4 (oca basse). L'amortissement associé
est donc plutôt faible par rapport aux autres causes, mais peut devenir
significatif pour des instruments à parois rugueuses (Sint
grand).
4) Puissance perdue du fait des pertes de charge dans les ouvertures de
l’ocarina
Pour évaluer ce terme, on admet que la perte de charge dans un trou
ouvert est donnée par l’expression
![]()
où v est la vitesse de l’air dans le trou (c’est
l’expression classique pour une perte de charge localisée)
Si on considère un système simple comme une bouteille (un goulot,
pas de trous latéraux), l'amortissement associé à la perte
de charge dans le goulot vaut :
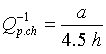
On remarque que le système est non-linéaire,
puisque l'amortissement dépend de l’amplitude a. A amplitude égale,
la dissipation est plus faible pour un ocarina raide, avec des cheminées
hautes.
Si on considère un ocarina oscillant avec une amplitude au goulot typique,
de 2mm, l'amortissement correspondant vaut Q-1 = quelques pourcents,
valeur non-négligeable.
Plus compliqué, considérons maintenant un ocarina avec une fuite,
modélisée sous forme d’une deuxième ouverture (notée
avec l’indice f dans le formalisme qui suit, alors que les variables et
paramètres liés au goulot portent l’indice e).
L'amortissement dû à la fissure vaut :
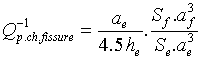
Si on suppose que la section de fuite Sf est petite devant la section du goulot Se, af=ae*he/hf. L’amplitude du mouvement de l’air au travers de la fissure est alors inversement proportionnelle à la hauteur de la cheminée, et ne dépend pas de la surface de la fissure. Dans ces conditions, l'amortissement dû aux pertes de charge dans la fissure vaut alors :
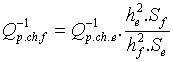
On notera que cette quantité peut devenir grande si
hf est petit et Sf grand (fuite importante en paroi mince).
Cette expression permet de comprendre pourquoi une fissure ou une fuite dans
un ocarina peut empêcher celui-ci de parler : si la fuite est importante
et en paroi mince, l'amortissement devient grand et peut amener l’instrument
au dessous du seuil d’auto entretien.
5) Puissance perdue par mise en vibration des parois du
résonateur.
Cet effet est mentionné ici pour mémoire, car dans la suite, on
supposera que l'ocarina possède des parois parfaitement rigides. Il n'en
reste pas moins qu'en réalité, les ocarinas faits avec des parois
minces (papier, carton) parlent moins facilement que ceux faits en matériaux
rigides.
En additionnant toutes les causes d'amortissement, les considérations
ci-dessus permettent de prédire que le coefficient d'amortissement global
d'un ocarina typique est de l'ordre de quelques %, les causes prépondérantes
étant les pertes par rayonnement et les pertes de charge aérodynamiques
dans les trous ouverts et (peut-être) les transferts de chaleur à
la paroi.
L'amortissement d'une flûte de même fréquence sera notablement
inférieur : pour une même amplitude de l'oscillation au niveau
des ouvertures, la puissance dissipée par rayonnement et par perte de
charge est la même dans les deux instruments, mais l'énergie stockée
dans la flûte est plus grande, dans un rapport h/L égal à
la longueur du goulot de l'ocarina sur la longueur de la flûte.
Evaluation expérimentale de la surtension-dissipation d'un ocarina
Compte-tenu de la définition de la surtension, le temps mis
par une oscillation libre du résonateur pour s'atténuer d'un facteur
e en intensité (et donc d'un facteur e**1/2 en amplitude) est
![]()
Le temps ![]() correspond à une atténuation sur l'amplitude de 10.log(e) = 4.34
dB.
correspond à une atténuation sur l'amplitude de 10.log(e) = 4.34
dB.
Pour un musicien, ![]() est le temps pendant lequel l'instrument "vibre encore" après qu'on ait
cessé de souffler dedans. Pour un instrument à vent typique, la
surtension est de l'ordre de 20, et le temps
est le temps pendant lequel l'instrument "vibre encore" après qu'on ait
cessé de souffler dedans. Pour un instrument à vent typique, la
surtension est de l'ordre de 20, et le temps ![]() de l'ordre de quelques dizaines de millisecondes.
de l'ordre de quelques dizaines de millisecondes.
Il existe des logiciels de décomposition spectrale par transformée
de Fourier rapide qui permettent de mesurer l'amplitude en dB de chaque composante
spectrale d'un son en fonction du temps. Quand on interrompt brutalement l'autoentretien,
les composantes spectrales s'éteignent les unes après les autres,
en commençant par celles de plus haute fréquence. On suppose que
le temps de décroissance de la composante spectrale de plus basse fréquence
est gouverné par l'atténuation du mode propre correspondant du
résonateur.

Le spectre d'un son d'ocarina, sur un ré2 joué crescendo. On
constate la présence d'harmoniques dans le spectre. Ces harmoniques sont
beaucoup moins nombreux que dans un son de flûte, mais ils sont bien présents
et sortent d'autant plus que le son est plus fort. On en conclut qu'ils sont
imputables aux non linéarités de l'auto-entretien.
Quand on cesse de souffler dans l’ocarina, le son ne s’éteint
pas immédiatement, et c’est le fondamental qui disparaît
en dernier.
La décroissance mesurée pour chaque composante
spectrale est exponentielle, et se traduit par un diagramme amplitude-temps
linéaire, l'amplitude de chaque composante étant exprimée
en dB. La pente de cette droite permet de calculer ![]() ,
et donc la surtension Q ou l'amortissement Q-1.
,
et donc la surtension Q ou l'amortissement Q-1.
Pour que la mesure soit correcte, il faut que l'autoentretien s'interrompe brutalement,
dans un temps petit devant le temps d'atténuation ![]() .
On peut vérifier si cette condition est bien remplie en examinant les
composantes de haute fréquence, qui décroissent très vite.
Un flûtiste entraîné semble pouvoir interrompre son souffle
en moins de dix millisecondes, ce qui rend la mesure de
.
On peut vérifier si cette condition est bien remplie en examinant les
composantes de haute fréquence, qui décroissent très vite.
Un flûtiste entraîné semble pouvoir interrompre son souffle
en moins de dix millisecondes, ce qui rend la mesure de ![]() possible sans déconvolution.
possible sans déconvolution.
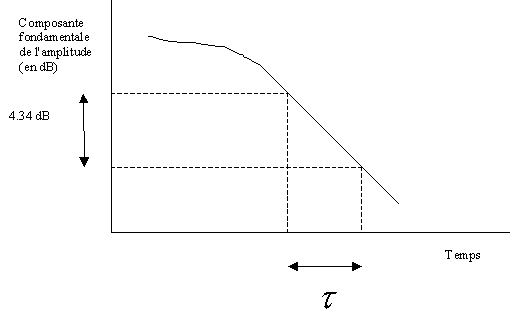
Les coefficients d'amortissement d'un même sol grave
d'ocarina alto et de flûte à bec ténor ont été
mesurées par cette méthode. Le temps d'atténuation τ
vaut respectivement 6 et 12 ms pour ces deux instruments, ce qui donne des coefficients
de surtension de 16 et 32 respectivement, ou encore des coefficients d'atténuation
de 6% et 3% respectivement. Ces valeurs sont du même ordre de grandeur
que celles prédites par la théorie. Il est également satisfaisant
de constater que, comme prévu, l'amortissement de la flûte est
inférieur à celui de l'ocarina. Compléter, et donner
ici l'ordre de grandeur de l'amortissement mesuré pour des ocarinas différents.
Le seuil d'autoentretien se traduit-il par une valeur limite
du coefficient d'atténuation ?
Des expériences simples semblent le suggérer : par exemple, une
flûte en carton ne sonne en général pas du tout. Une bouteille
en verre produit facilement un son si on l’utilise comme un résonateur
de Helmholtz excité en soufflant sur son goulot. Une bouteille d’eau
minérale en plastique parle déjà moins facilement parce
que ses parois sont plus souples et absorbent une partie de l'énergie
vibratoire stockée dans l'air de la bouteille. La même bouteille
déformée en la pinçant entre deux doigts jusqu’à
faire fléchir la paroi vers l’intérieur refusera obstinément
de produire le moindre son. En inversant localement la courbure de la paroi,
on crée près du point d’appui des zones de faible courbure,
où la paroi est encore plus souple qu'ailleurs, et amortit beaucoup les
vibrations. L’amortissement passe alors au dessus du seuil au delà
duquel l’autoentretien du son devient impossible. Tout en continuant de
souffler, il suffit de relâcher la paroi pour que le son renaisse. Il
est difficile de déterminer le seuil d'autoentretien à partir
des premiers principes. On ne peut guère faire que de la phénoménologie
dans ce domaine, et cette phénoménologie reste à affiner
par des expériences détaillées. En tous cas, pour une embouchure
de flûte, l'autoentretien ne semble guère possible pour des coefficients
d'amortissement supérieurs à 10%. Les ocarinas représentent
des systèmes idéaux pour l'étude expérimentale de
ce seuil, dans la mesure où leur amortissement est facile à évaluer,
et à modifier.
Une mesure du seuil d’autoentretien sur un ocarina
Je souffle dans une bouteille de verre de 33 cl, et j'analyse le spectre du
son de goulot de ce résonateur. La mesure du temps de décroissance
de la résonance donne accès à l'amortisement, via la méthode
décrite plus haut. J’introduis ensuite dans la bouteille des morceaux
de coton, et je recommence la mesure du coefficient d'amortissement. J’ajoute
du coton jusqu’à ce que la bouteille refuse de parler. Le seuil
d’autoentretien ainsi déterminé correspond à une
surtension d’environ Q = 8 ou un coefficient d'amortissement de 1/8, soit
12.5%. En principe, ce seuil dépend de la géométrie de
l’embouchure, et d’elle seule. Il reste à voir si le seuil
dépend fortement ou non de la géométrie, en recommençant
l’expérience avec divers goulots à embouchure de flûte
à bec, rapportés sur un même récipient.
Comment se comparent les amortissement d'un ocarina "raide" et d'un ocarina
"mou"?
Considérons deux ocarinas de même fréquence, et possédant
la même section de goulot : l'un raide (goulot haut, volume de résonateur
faible), l'autre mou (goulot bas, résonateur de grand volume).
Ocarina "raide" |
Ocarina "mou" |
|
 |
||
| Amortissement de rayonnement Q-1ray | Faible |
Fort |
| Amortissement dû à la perte de charge dans le goulot Q-1 p.ch: | Faible |
Fort |
| Amortissement dû à la non adiabaticité du volume gazeux Q-1 n.a gaz : | identique sur les deux ocarinas |
|
| Amortissement dû aux transferts de chaleur gaz-paroi Q-1 na paroi : | Fort |
Faible |
Globalement, l'ocarina raide aura un amortissement du même ordre que l'ocarina
mou de même fréquence. Cependant, j'ai observé qu'il parlait
moins bien. Peut-être est-ce dû à la proximité des
modes propagatifs?
Influence de l’échelle sur l'amortissement de l’ocarina
: amortissement comparé d'un ocarina grave et d'un ocarina aigu homothétiques.
Ocarina aigu |
Ocarina grave |
|
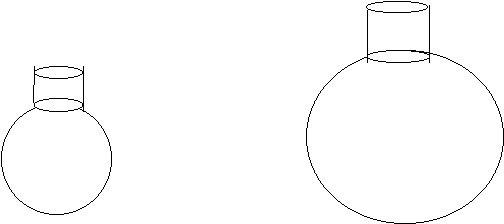 |
||
| Amortissement de rayonnement Q-1ray | identique sur les deux ocarinas.
|
|
| Amortissement dû à la perte de charge dans le goulot Q-1 p.ch: | identique sur les deux ocarinas |
|
| Amortissement dû à la non adiabaticité du volume gazeux Q-1 n.a gaz: l'amortissement du son dans l'air libre est plus fort dans l'aigu | Fort |
Faible |
| Amortissement dû aux transferts de chaleur gaz-paroi Q-1 na paroi : | Faible |
Fort |
Globalement, l'ocarina aigu aura un amortissement du même ordre que l'ocarina
grave. Cependant, on ne peut rien en conclure sur la facilité d'émission
comparée pour des ocarinas graves et aigus, car le seuil d'autoentretien
dépend probablement de la fréquence (essais à faire).
Fabrication des ocarinas
Je ne décris pas ici la fabrication des ocarinas traditionnels en terre
cuite, mais une méthode de fabrication beaucoup plus facile, accessible
aux artisans-amateurs.

En haut de la photo : le corps du résonateur.
En bas : l'embouchure.
Il est possible de réaliser facilement des embouchures qui sonnent bien selon le modèle ci-dessus : une échancrure taillée en biseau dans un bout de tube, et un porte-vent fait de deux morceaux de bois collés sur le tube et assemblés entre eux de façon à laisser une lumière pour le jet d'air. L’ensemble joue le rôle d'un goulot, qui s’insère facilement dans le volume du récipient de l’ocarina.
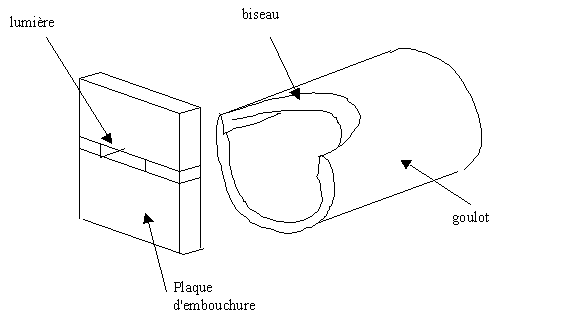
Premier type d'embouchure. L'échancrure du biseau est faite d'un coup
de lime ronde. Le porte-vent est fait de deux plaques de bois assemblées
en laissant entre elles une lumière.
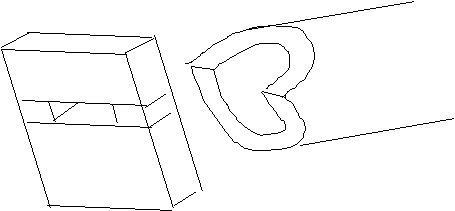
Deuxième type d'embouchure, encore plus facile à fabriquer.
Le porte-vent est identique au précédent. Le biseau du tube
est fait de deux coups de scie à 45°.
On peut fabriquer le volume de l’ocarina dans un bout
de tube PVC fermé aux deux extrémités par une plaque de
bois.
Les cheminées latérales (trous de jeu bouchés par les doigts)
peuvent être faites par insertion dans le volume de l’ocarina de
bouts de tube de longueur et de diamètre intérieur déterminés.
Cet arrangement permet tous les tâtonnements de justesse, puisqu’il
reste possible de changer à tout moment la longueur et le diamètre
des cheminées. On a intérêt à avoir des trous latéraux
d'un diamètre à peu près uniforme, pour pouvoir les boucher
commodément. Les premiers trous de l'ocarina (ceux du bas de la gamme)
devront avoir une hauteur de cheminée importante, les derniers (ceux
du haut) une hauteur de cheminée faible. L'intérêt des inserts
est de pouvoir réaliser des cheminées de hauteur choisie, dans
un tube à parois minces.
Avec ces quelques recettes simples, j’ai pu réaliser en peu de
temps des ocarinas de toutes hauteurs, justes et qui sonnent bien. La modularité
et l'interchangeabilité des éléments de l'ocarina facilitent
beaucoup la mise au point.
Seule précaution importante : attention à l’étanchéité
des collages : la moindre fuite empêchera l’ocarina de parler
(on a vu pourquoi au § "Amortissement").
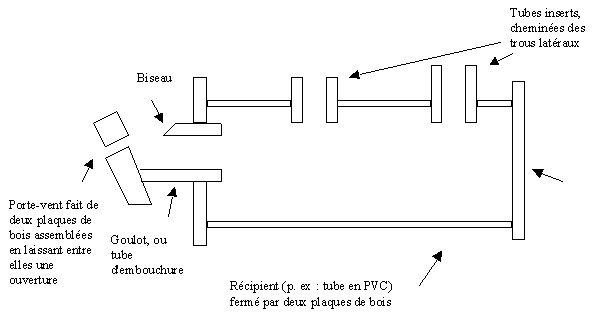
Schéma d'un ocarina fabriqué selon la méthode
décrite ci-dessus

Quelques règles simples sur les proportions de l'ocarina
:
La distance lumière-biseau est un paramètre important sur
un ocarina. La règle de base, applicable à tous les instruments
à embouchure de flûte, est que la fréquence propre d’oscillation
du jet " seul " doit être proche de la fréquence
propre du résonateur (cf eq. 5). Si on veut un instrument qui parle bien,
on pourra respecter l’ordre de grandeur suivant pour la distance lumière-biseau :
| Soprano | Alto | Ténor | Basse | Contrebasse | |
| Pulsation centrale de l’instrument (rd/s) | 5000 | 3770 | 2500 | 1880 | 1250 |
| Distance lumière-biseau (mm) | 5 à 8 | 7 à 10 | 9 à 15 | 10 à 16 | 11 à 17 |
Cette distance lumière-biseau croît moins vite
que 1/ω. C'est pourquoi les dimensions d'un ocarina basse ne se dιduisent
pas de celles d'un ocarina soprano par simple homothétie. Pour respecter
la contrainte sur la distance lumière-biseau, l'ocarina doit présenter
au niveau de la lucarne d'embouchure un rétrécissement d'autant
plus marqué que l'ocarina est plus grave.
Abaque donnant la pulsation d'un ocarina en fonction de ses dimensions principales
(volume, rapport surface sur hauteur du goulot).
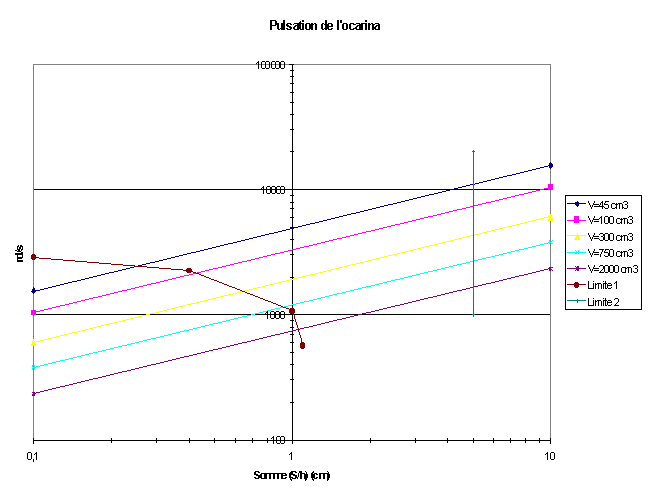
Les cinq droites parallèles du diagramme correspondent respectivement
à des ocarinas soprano, alto, ténor, basse et contrebasse.
Le volume de l’ocarina n’étant pas ajustable,
c’est la quantité Somme (S/h) qui varie pour faire les différentes
notes de la tessiture. D'après l'éq. 1, Somme (S/h) doit varier
d’un facteur 4 entre le grave et l’aigu, pour un ocarina doté
d’une étendue d’une octave.
Quand la paroi de l’ocarina est fine, le rapport Somme (S/h) est maximal,
et vaut approximativement Σ(d), somme des diamθtres des trous ouverts.
La partie gauche de la courbe correspond à des ocarinas raides, dotés
d’un champ de liberté étroit ; la partie droite à
des ocarinas mous.
Dans la zone située à gauche sous la courbe en noir (limite 1),
l’ocarina ne parle pas car son amortissement est excessif, ou parle mal
car on excite aussi les modes propagatifs.
Dans la zone située à droite, au delà de Somme (S/h) =
5 cm (limite 2), l’ocarina n’est plus jouable car les trous sont
trop gros pour être bouchés avec les doigts. En effet, un accroissement
de fréquence de 1 ton correspond à un deltaω/ω
de 0.12, et doit κtre associé à un accroissement double
de Somme (S/h). Par conséquent, si on veut que le dernier trou de jeu
débouché fasse monter le son d’un ton, il faut que delta(Somme
(S/h))/(Somme (S/h)) = 0.24. Pour que l’ocarina soit jouable, il faut
que l’accroissement en Somme (S/h) associé au débouchage
de ce dernier trou soit inférieur à 1 à 1.5 cm, sinon,
on ne peut pas boucher ce trou avec le doigt. Donc, le (Somme (S/h)) total maximum
vaut 1 à 1.5/0.24 soit 4 à 6 cm, d’où la limite citée
plus haut.
On voit que la zone praticable pour les instruments graves se réduit
au point de rendre les ocarinas de fréquence très grave irréalisables
dans la pratique, sauf à réduire leur tessiture à quelques
notes, avec des trous latéraux de grand diamètre, bouchés
par des clés ou par la paume de la main. Il faudra également penser
à employer des musiciens dotés de vastes poumons !
Plans complets de quelques ocarinas, avec leur table de doigtés.
Pour ceux que les calculs ennuient, que les tâtonnements lassent,
et qui veulent obtenir directement un ocarina qui marche, voici les dimensions
principales de quelques instruments :
| Soprano (ut) |
Alto (fa) |
Ténor (ut) |
Basse (fa) |
|
| Volume (cm3) |
45 |
100 |
300 |
750 |
| Longueur géométrique de col hc (cm) |
2.1 |
4 |
3 |
2.5 |
| Diamètre géométrique de col (cm) |
1.5 |
1.9 |
2.5 |
2.5 |
| Distance lumière-biseau l (mm) |
7 |
9 |
14 |
15 |
| Largeur du porte-vent g (mm) |
13.5 |
17.5 |
22.5 |
22.5 |
| Surface de la lucarne d'embouchure Se (cm2) |
0.9 |
1.15 |
2 |
2 |
| Hauteur géométrique de la lucarne d'embouchure he géom(mm) |
2 |
2 |
3 |
3 |
| 1er trou de jeu :
|
3.9; 7.5 |
3.9; 7.5 |
5.8; 9 |
5.8; 8 |
| 2ème trou de jeu |
5.8; 15 |
5.8; 15 |
5.8; 7 |
5.8; 6 |
| 3ème trou de jeu |
5.8; 8 |
5.8; 8 |
10.5; 13 |
10.5; 13 |
| 4ème trou |
5.8; 35 |
5.8; 35 |
5.8; 30 |
5.8; 16 |
| 5ème trou |
5.8; 6.5 |
5.8; 6.5 |
10.5; 14 |
10.5; 12 |
| 6ème trou |
8; 10 |
8; 10 |
12; 11 |
12; 10 |
| 7ème trou |
10.5; 10 |
10.5; 10 |
15; 9 |
15; 8 |
| 8ème trou |
10.5; 5 |
10.5; 5 |
15; 4 |
15; 3 |
Les plans ci-dessus correspondent à une table des doigtés, donnée
ci-dessous pour un ocarina en ut (pour les instruments en fa, il suffit de transposer
la hauteur de toutes les notes d'une quarte). Pour faciliter le jeu, les ocarinas
ci-dessus ont été conçus avec une table de doigtés
identique à celle des flûtes à bec, doigté "baroque".
TABLE DES DOIGTES (pour un ocarina en ut)
Les trous de jeu (8 au total) sont numérotés ainsi :
1 = auriculaire main droite
2 = annulaire MD
3 = majeur MD
4 = index MD
5 = annulaire MG
6 = majeur MG
7 = index MG
8 = pouce MG
( 0= trou ouvert; 1= trou bouché).
| Trou n° | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Do | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Ré | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Ré# | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| Mi | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| Fa | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| Fa# | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| Sol | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Sol# | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| La | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| La# | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| Si | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| Do | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| Do# | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
NB : il est très facile de faire d'autres ocarinas
sans suivre ces plans aveuglément. Un des charmes de cet instrument,
c'est justement de se prêter à tous les tâtonnements, et
d'être accessible aux artisans amateurs…
Pour accorder un ocarina
Un ocarina ayant une étendue d'une octave seulement, chaque doigté
commande une seule note. Avec presque autant de trous que de notes dans la tessiture,
l'accord d'un ocarina est notablement plus simple que l'accord d'une flûte.
Il est aussi moins crucial : dans la mesure où le champ de liberté
en fréquence est plus grand que sur une flûte, il sera toujours
possible d'ajuster la hauteur en soufflant plus ou moins fort pour jouer juste.
Voici comment on peut procéder pour accorder un ocarina : accorder d'abord
la note de base en faisant varier le volume du récipient, l'ouverture
de l'embouchure, ou la longueur du col. Accorder ensuite les notes suivantes,
en partant du bas de la gamme, et tout d'abord la note correspondant au premier
trou de jeu débouché. L'accord pourra se faire en ajustant le
diamètre du trou ou la hauteur de la cheminée (l'opération
est facile si on a choisi de faire les cheminées latérales par
insertion de petits tronçons de tubes dans le corps du résonateur.
Il suffit dans ce cas de couper ou de limer ces bouts de tube).
Une fois l'accord obtenu sur cette note, passer à celle imédiatement
au dessus, correspondant à deux trous de jeu débouchés,
en jouant de la même manière sur la géométrie (diamètre,
hauteur de cheminée) du deuxième trou.
Continuer avec le troisième trou, et ainsi de suite jusqu'en haut de
la gamme.
Dans cette méthode, les notes correspondant aux doigtés de fourche
(ré#, fa#, sol#, la# pour un ocarina en ut) ne sont pas accordées.
L'expérience montre que ce n'est pas très grave.
Une fois l'accord global obtenu sur toute l'étendue de l'instrument,
les puristes remarqueront que le volume de l'ocarina a été modifié
par le perçage des trous de jeu, et que la note de base s'en trouve légèrement
abaissée. Il est toujours possible de faire un "deuxième tour"
d'accord pour remonter les notes du bas de la gamme, mais la correction est
en général très faible, et peut être jugée
superflue.
Helmholtz et Larsen
Peut-on faire de la musique "électroacoustique" en contrôlant l'effet
Larsen dans un ocarina? Avec le dispositif suivant (boucle micro dans le résonateur-ampli-haut
parleur proche du résonateur), la fréquence auto amplifiée
est celle du résonateur. Il suffit de doter le résonateur de trous
latéraux pour modifier sa fréquence, et donc celle produite par
la boucle. Plus besoin de souffler dans l’ocarina, l’électronique
fait le travail ! L’ennui est que le temps de montée des transitoires
est lent et mal maîtrisé : on ne peut pas avoir de véritables
attaques avec cet instrument, sauf peut-être en frappant le résonateur
(à essayer).
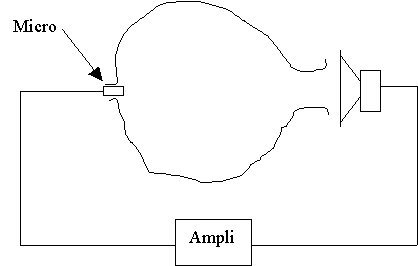
Une boucle électronique pour contrôler la fréquence de
l'effet Larsen
Pourrait-on fabriquer des ocarinas à anche solide?
Pourquoi pas? L'intérêt serait de trouver des timbres d'instruments
inédits. En couplant une anche solide à un résonateur de
Helmholtz, on attend un timbre plus rond, et plus pauvre en harmoniques que
celui de tuyaux munis des mêmes systèmes excitateurs.
Avec une anche solide, les paramètres d'oscillateur MA, KA
de l'anche seront beaucoup plus grands que ceux associés à un
jet d'air. La fréquence propre du système sera énormémént
influencée par l'anche, bien plus qu'avec un tuyau car dZT/dω
est plus petit (cf paragraphe sur le couplage au jet). Plus besoin de trous
de jeu : tous les glissandos seront permis!
J'ai essayé de raccorder un bec de clarinette à une bouteille
(percée au fond, sinon on ne peut pas souffler dans l'embouchure!). ça
donne un son joliment coloré, mais l'instrument est d'un contrôle
difficile car le champ de liberté en fréquence est très
grand.
Il faut également faire attention aux modes propagatifs de goulot, ou
plus généralement, aux modes propres d'ordre supérieur
du résonateur. Par exemple, avec un goulot long, l'anche a tendance à
exciter ces modes, ce qui fait faire des canards à l'instrument. Pour
les éviter, il faut respecter deux contraintes :
1) La fréquence propre du résonateur doit être située
dans le domaine de fréquences excitables par l'anche (donner la fourchette
pour différents types d'anche).
2) Il faut éviter les discontinuité brutales de section entre
le tube qui porte l'anche et le goulot du résonateur. Un évasement
progressif du goulot permettra une meilleure adaptation d'impédance entre
l'anche et le résonateur.
Qu'est ce que ça donnerait avec une anche de hautbois? Avec une embouchure
de tuba? Il en reste, des choses à explorer!
Annexe : Un programme pour calculer la justesse
des ocarinas.
Pour ceux qui se fient au calcul : les équations de cet article ont été
rassemblées dans un logiciel "ocarina3" (à télécharger
ici avec ses fichiers de données), qui permet de calculer la justesse
d’un ocarina, connaissant sa géométrie et sa table de doigtés.
Il tient compte du couplage au jet. Ses résultats ont été
validés par de nombreuses comparaisons avec l’expérience.
Il peut aider celui qui veut concevoir sans tâtonner des ocarinas de forme,
tessiture ou doigtés variés.
Le fichier d'entrée (qui doit s'appeler oca.dat) contient toutes
les données géométriques de l'instrument.
Voici un exemple de fichier d'entrée correspondant à l'ocarina
basse dont les caractéristiques ont été données
au § "Plans" (dans ce fichier, toutes les unités sont SI) :
oca basse en fa, doigté de flute à bec oca3
PARAMETRES PHYSIQUES DE L' AIR :RHOA,P0,GAMMA,CV,ETA,TONEW,DLAMBA
1.204 1.014E5 1.400 719. 1.8E-5 11.7 2.4E-2
volume du resonateur (trous non compris) v0
750.e-6
NOMBRE DE TROus de jeu (-1) N
8
TABLEAU diametre des trous lateraux dp (DIMENSION N)
5.8e-3 5.8e-3 10.5e-3 5.8e-3 10.5e-3 12.e-3 15.e-3 15.e-3
TABLEAU hauteur des cheminees lp0 (DIMENSION N)
8.e-3 6.e-3 13.e-3 16.e-3 12.e-3 1.e-2 8.e-3 3.e-3
TABLEAU STYLE DES CLES ISTYLE (DIMENSION N)
0 0 0 0 0 0 0 0
TABLEAU LEVEE DES CLES LEVEE (DIMENSION N)
0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
FREQUENCE DU LA DE REFERENCE FLA
440.
TESSITURE NTESS, NTESSB
15 16
TABLE DES DOIGTES DOIGTE(I,J) (NTESS LIGNES, N COLONNES)
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 0 1 1 1 1 1 1
0 0 1 1 1 1 1 1
0 1 0 1 1 1 1 1
0 1 0 0 1 1 1 1
0 0 0 0 1 1 1 1
0 0 1 1 0 1 1 1
0 0 0 0 0 1 1 1
0 0 1 1 0 0 1 1
0 0 0 0 0 0 1 1
0 0 0 0 0 1 0 1
0 0 0 0 0 1 1 0
0 0 0 0 0 0 1 0
diamètre col, hauteur géom col, hauteur géom lucarne, surface
lucarne
25.e-3 2.5e-2 3.e-3 2.e-4
DONNEES CONCERNANT L' EMBOUCHURE
IFLUTE FCM FCP d0 LA0 alpha E0 V0 V1 LEVRES PAREMB
0 1. 0. 0.0225 15.e-3 2.1 5.5e-4 15. 5. 0. 0.
Au lancement du programme ocarina3.exe, une boîte de dialogue s'ouvre
pour déterminer quel degré de la gamme on veut calculer : répondre
1 si on veut calculer la note de base de l'ocarina (un do pour un ocarina en
ut), 8 si on veut calculer le 8ème degré (un sol sur
un ocarina en ut); répondre 0 si on veut calculer d'un coup l'ensemble
des notes de la tessiture. L'exécution du programme ocarina3.exe crée
un fichier de sortie appelé ocarina.out qui contient toutes les informations
sur les résultats.